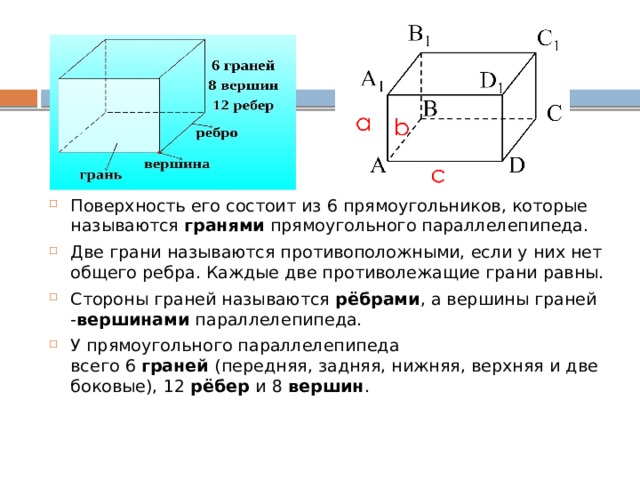
Параллелепипед – одна из основных геометрических фигур в трехмерном пространстве. Отличительной особенностью этого тела является то, что его грани формируют параллелограммы. Параллелепипед широко применяется в различных областях жизни, начиная от строительства и заканчивая промышленностью и научными исследованиями.
Площадь поверхности параллелепипеда – одна из наиболее важных характеристик данной фигуры. Она вычисляется путем сложения площадей всех его граней. Величина площади поверхности параллелепипеда позволяет определить, сколько площади занимает его внешняя часть.
Для вычисления площади каждой грани параллелепипеда необходимо знать длины его ребер. Например, площадь одной из граней параллелепипеда можно вычислить, умножив длину одного ребра на длину другого ребра. Затем результат необходимо умножить на синус угла между этими ребрами. Аналогичное действие выполняется для каждой грани параллелепипеда. Полученные значения площадей граней суммируются, что позволяет определить площадь поверхности параллелепипеда.
Определение площади параллелепипеда
Что такое параллелепипед и его характеристики
Определение
Параллелепипед – это выпуклое тело, ограниченное шестью параллельными прямоугольными гранями. Углы между гранями всегда равны 90 градусов.
Формула площади поверхности
Площадью поверхности параллелепипеда называется сумма площадей всех его граней. Для параллелепипеда со сторонами a, b и c площадь поверхности вычисляется по формуле:
S = 2(ab + ac + bc)
Объем
Объем параллелепипеда вычисляется по формуле:
V = abc
Где a, b и c – длины сторон параллелепипеда.
Параллелепипеды широко используются в геометрии, физике, инженерии и многих других областях. Их форма и свойства делают их удобным объектом для изучения и применения в различных задачах.
Формула для расчёта площади поверхности параллелепипеда
Площадь поверхности = 2(ab + bc + ac).
Для примера, рассмотрим параллелепипед со сторонами a = 3 см, b = 4 см и c = 5 см.
Подставляя значения в формулу, получаем:
Площадь поверхности = 2(3 * 4 + 4 * 5 + 3 * 5) = 2(12 + 20 + 15) = 2 * 47 = 94 см².
Таким образом, площадь поверхности данного параллелепипеда составляет 94 квадратных сантиметра.
Объяснение каждого элемента формулы

Формула для вычисления площади поверхности параллелепипеда определяется следующим образом:
1. a
a — это длина одной из сторон параллелепипеда. В формуле все стороны параллелепипеда обозначены одной буквой, чтобы избежать путаницы. В данном случае, a обозначает длину одной из сторон.
2. b
b — это длина второй стороны параллелепипеда.
3. c
c — это длина третьей стороны параллелепипеда.
У параллелепипеда есть три измерения: длина, ширина и высота, которые обозначаются a, b и c соответственно. Для вычисления площади поверхности параллелепипеда нужно знать длины всех его сторон.
Площадь поверхности параллелепипеда может быть вычислена с помощью следующей формулы:
S = 2ab + 2bc + 2ac
Где S — это площадь поверхности параллелепипеда. Перемножение длин сторон параллелепипеда и их умножение на 2 осуществляется для того, чтобы учесть все его стороны и поверхности.
Например, если длина одной стороны параллелепипеда равна 10, длина второй стороны — 5, а длина третьей стороны — 3, то площадь поверхности можно вычислить по формуле:
S = 2 * 10 * 5 + 2 * 5 * 3 + 2 * 10 * 3 = 100 + 30 + 60 = 190
Таким образом, площадь поверхности параллелепипеда равна 190 квадратных единиц.
Примеры вычисления площади параллелепипеда
Рассмотрим несколько примеров вычисления площади параллелепипеда:
Пример 1:
Дан параллелепипед со сторонами a = 3, b = 4 и c = 5.
Применяем формулу: S = 2(3*4 + 4*5 + 3*5) = 2(12 + 20 + 15) = 2(47) = 94.
Площадь поверхности параллелепипеда равна 94.
Пример 2:
Дан параллелепипед со сторонами a = 2, b = 2 и c = 2.
Применяем формулу: S = 2(2*2 + 2*2 + 2*2) = 2(4 + 4 + 4) = 2(12) = 24.
Площадь поверхности параллелепипеда равна 24.
Пример 3:
Дан параллелепипед со сторонами a = 7, b = 5 и c = 3.
Применяем формулу: S = 2(7*5 + 5*3 + 7*3) = 2(35 + 15 + 21) = 2(71) = 142.
Площадь поверхности параллелепипеда равна 142.
Таким образом, площадь поверхности параллелепипеда можно вычислить, зная длины его сторон, используя формулу S = 2(ab + bc + ac).
Значение площади поверхности в различных областях
Параллелепипед, как геометрическое тело, имеет шесть граней. Площадь его поверхности может быть выражена суммой площадей этих граней. Значение площади поверхности параллелепипеда зависит от его размеров и формы.
Площадь поверхности прямоугольного параллелепипеда
Если все грани прямоугольного параллелепипеда являются прямоугольниками, то площадь его поверхности может быть найдена по формуле S = 2(ab + ac + bc), где a, b и c — длины его сторон.
Например, если прямоугольный параллелепипед имеет стороны a = 4 см, b = 6 см и c = 8 см, то его площадь поверхности равна S = 2(4*6 + 4*8 + 6*8) = 2(24 + 32 + 48) = 2(104) = 208 см².
Площадь поверхности куба
Куб — это параллелепипед, у которого все стороны равны. Если сторона куба равна a, то его площадь поверхности выражается формулой S = 6a².
Например, если сторона куба равна a = 5 см, то его площадь поверхности равна S = 6 * 5² = 6 * 25 = 150 см².
Таким образом, значение площади поверхности параллелепипеда зависит от его формы и размеров, и может быть найдено с использованием соответствующих формул. Это позволяет определить, сколько площади требуется покрыть при обработке или упаковке параллелепипеда, а также оценить его поверхностную площадь в контексте задач геометрии и физики.
Практическое значение площади поверхности параллелепипеда
В проектировании и строительстве, знание площади поверхности параллелепипеда позволяет определить количество материала, необходимого для отделки его стен и крыши. Архитекторы и дизайнеры используют площадь поверхности параллелепипеда для расчета нагрузки на фундамент и определения необходимого объема отопительных и вентиляционных систем.
В физике и инженерии, площадь поверхности параллелепипеда полезна при изучении теплопроводности материалов, разработке эффективных систем охлаждения и термоизоляции. Она также играет важную роль в оптике при расчете преломления света и зеркального отражения.
В информационных технологиях, площадь поверхности параллелепипеда может использоваться для определения необходимого объема памяти или мощности вычислительных систем.
Таким образом, площадь поверхности параллелепипеда имеет практическое значение во многих областях науки и техники, где требуется точное измерение поверхности объектов для расчетов и проектирования.
Для того чтобы вычислить площадь поверхности параллелепипеда, нужно найти площади каждой его грани и сложить их.
Параллелепипед состоит из шести граней – трех параллельных прямоугольников.
Площадь прямоугольника вычисляется как произведение его длины на ширину.
Таким образом, площадь поверхности параллелепипеда равна сумме площадей всех его граней, то есть:
- площадь основания,
- площадь верхней грани,
- площадь передней грани,
- площадь задней грани,
- площадь левой боковой грани,
- площадь правой боковой грани.
Понимание площади поверхности параллелепипеда позволяет решать различные задачи, связанные с его конструкцией и использованием.
Вопрос-ответ:
Что такое площадь поверхности параллелепипеда?
Площадью поверхности параллелепипеда называют сумму площадей всех его граней.
Как вычислить площадь поверхности параллелепипеда?
Для вычисления площади поверхности параллелепипеда необходимо умножить периметр основания на высоту и прибавить удвоенную сумму площадей боковых граней.
Для чего нужно знать площадь поверхности параллелепипеда?
Знание площади поверхности параллелепипеда позволяет нам рассчитывать необходимое количество материала для его облицовки, а также для решения других задач, связанных с пространственной геометрией.
Какая формула используется для вычисления площади поверхности параллелепипеда?
Формула для вычисления площади поверхности параллелепипеда зависит от его размеров. Если известна длина, ширина и высота параллелепипеда, то площадь поверхности можно вычислить по формуле S = 2*(a*b + b*c + a*c), где a, b и c — соответствующие стороны параллелепипеда.
Можно ли узнать объем параллелепипеда, зная только его площадь поверхности?
Нет, нельзя узнать объем параллелепипеда, зная только его площадь поверхности. Для вычисления объема необходимо знать все три измерения (длину, ширину и высоту) параллелепипеда.