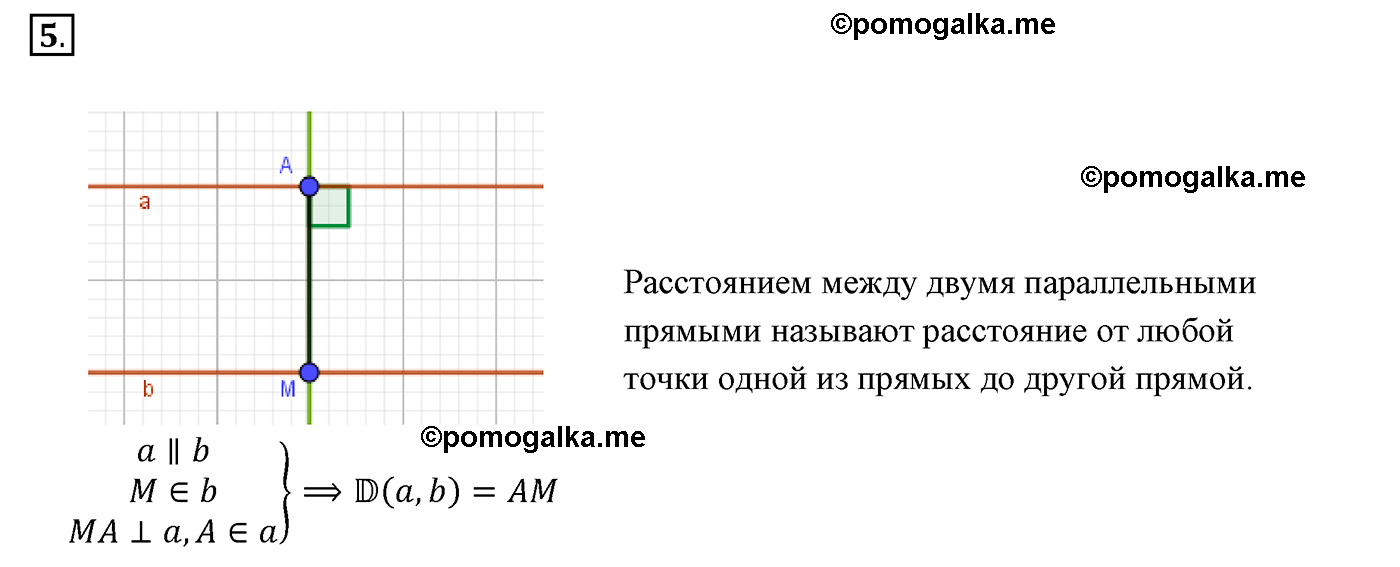
Параллельные прямые – это прямые, которые не пересекаются ни в одной точке. Расстояние между двумя такими прямыми – одна из важных характеристик, которая помогает определить, насколько близко или далеко прямые находятся друг от друга.
Расстояние между двумя параллельными прямыми можно вычислить с помощью геометрических формул. Одна из самых простых формул для расчета расстояния между параллельными прямыми основана на использовании перпендикуляра. Перпендикуляр – это прямая, которая образует с другой прямой угол в 90 градусов. Чтобы найти расстояние между двумя параллельными прямыми, можно провести перпендикуляр из точки одной прямой на другую и измерить его длину.
Также существуют другие методы для определения расстояния между параллельными прямыми, например, использование векторов или уравнения прямых. Расстояние между прямыми может быть положительным или отрицательным, в зависимости от направления проведенного отрезка. Незав-исимо от способа вычисления, расстояние между двумя параллельными прямыми является важным инструментом в геометрии и находит применение в различных областях, таких как архитектура, инженерия и физика.
Расстояние между двумя параллельными прямыми: основные понятия
Для нахождения расстояния между двумя параллельными прямыми необходимо знать координаты точек, через которые эти прямые проходят. Обозначим эти точки как A(x₁, y₁) и B(x₂, y₂). Для удобства, можно представить эти точки в виде таблицы:
| Точка | x | y |
|---|---|---|
| A | x₁ | y₁ |
| B | x₂ | y₂ |
Расстояние между двумя параллельными прямыми можно вычислить с помощью формулы:
d = |Ax + By + C| / √(A² + B²),
где A, B и C — коэффициенты уравнения прямой, Ax + By + C = 0.
Здесь знак модуля | | обозначает абсолютное значение числа. Радикал (√) — это знак квадратного корня.
При нахождении расстояния между двумя параллельными прямыми, необходимо учитывать знаки коэффициентов A, B и C, так как они могут быть положительными или отрицательными.
Определение расстояния между двумя параллельными прямыми имеет важное практическое применение в различных областях, таких как геометрия, физика и инженерия. Например, при проектировании зданий и строительстве, знание расстояния между параллельными стенами может помочь определить ширину помещений и расположение объектов внутри.
Определение расстояния между двумя параллельными прямыми
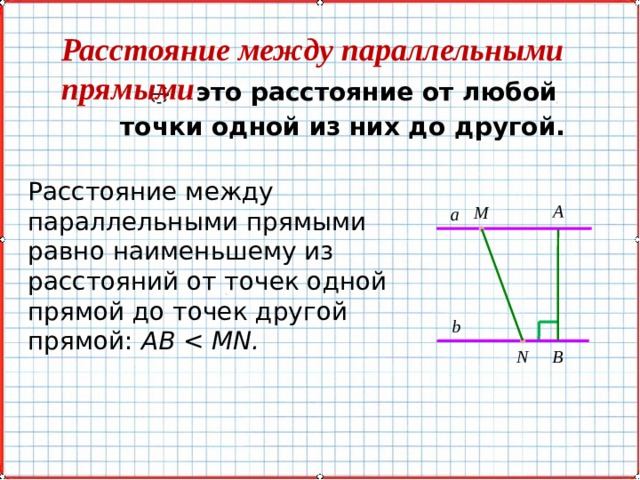
Для определения расстояния между параллельными прямыми мы можем использовать геометрические свойства этих прямых. Если две прямые параллельны, то все перпендикулярные к ним прямые также параллельны. Таким образом, мы можем провести прямую линию, которая будет перпендикулярна и к одной, и к другой параллельной прямой.
Чтобы найти расстояние между двумя параллельными прямыми, мы можем взять одну из перпендикулярных прямых и измерить длину отрезка между ними. Такое измерение будет являться искомым расстоянием между двумя параллельными прямыми.
Зная уравнения двух параллельных прямых, мы можем использовать формулу расстояния между двумя точками для определения длины отрезка между этими прямыми. Формула расстояния между двумя точками выглядит следующим образом:
d = √((x2 — x1)^2 + (y2 — y1)^2)
Где (x1, y1) и (x2, y2) — координаты двух произвольных точек на прямых. Подставляя координаты двух точек на параллельных прямых в эту формулу, мы получим искомое расстояние между ними.
Таким образом, расстояние между двумя параллельными прямыми можно определить с использованием геометрических свойств прямых и формулы расстояния между двумя точками. Это измерение играет важную роль в геометрии и на практике может использоваться для решения различных задач, связанных с прямыми и их взаимным расположением.
Построение перпендикуляра к параллельным прямым
- Выберите точку на одной из параллельных прямых, которая будет служить началом построения перпендикуляра. Обозначим эту точку как A.
- С помощью циркуля или риска на линейке проведите дугу из точки A, чтобы она пересекала обе параллельные прямые. Назовем пересечение дуги с прямыми точками B и C соответственно.
- Соедините точки B и C линией. Эта линия будет перпендикулярна к параллельным прямым AB и AC.
Таким образом, используя простейшие геометрические инструменты, мы можем построить перпендикуляр к параллельным прямым.
Методы измерения расстояния между двумя параллельными прямыми
Расстояние между двумя параллельными прямыми можно измерить различными способами. Рассмотрим несколько методов:
1. Использование перпендикулярной прямой. Для этого проводят перпендикулярную прямую к одной из параллельных прямых. Затем измеряют расстояние от перпендикулярной прямой до другой параллельной прямой. Полученная величина будет равна расстоянию между параллельными прямыми.
2. Использование формулы для вычисления расстояния. Если известны координаты точек на параллельных прямых, можно применить формулу для вычисления расстояния между двумя точками в прямоугольной системе координат. Для этого нужно найти разницу между координатами соответствующих точек на параллельных прямых и применить формулу sqrt((x2 — x1)^2 + (y2 — y1)^2), где (x1, y1) и (x2, y2) — координаты точек.
3. Использование таблицы. Для измерения расстояния между параллельными прямыми можно построить таблицу, где в первом столбце указать значения x на прямой, а во втором столбце — значения y на прямой. Затем вычислить разность значений y для соответствующих значений x и найти ее модуль. Полученная величина будет равна расстоянию между параллельными прямыми.
Таким образом, существует несколько методов измерения расстояния между двумя параллельными прямыми, каждый из которых имеет свои преимущества и может быть использован в различных ситуациях.
Расстояние между параллельными прямыми на плоскости
Для вычисления расстояния между параллельными прямыми можно использовать следующую формулу:
- Выберите любую точку на одной из параллельных прямых и обозначьте ее координатами x1 и y1.
- Выберите любую точку на другой параллельной прямой и обозначьте ее координатами x2 и y2.
- Используя формулу для вычисления расстояния между двумя точками в декартовой системе координат, найдите расстояние между выбранными точками.
Итак, расстояние между параллельными прямыми на плоскости равно длине отрезка, соединяющего любые две точки, одна из которых лежит на одной прямой, а другая — на параллельной ей прямой.
Это понятие широко используется в различных областях, таких как строительство, графика, физика и другие. Знание расстояния между параллельными прямыми позволяет решать задачи, связанные с определением геометрических параметров или нахождением оптимальных решений.
Теперь вы знакомы с понятием расстояния между параллельными прямыми на плоскости. Пользуйтесь этой информацией для успешного решения геометрических задач и развития в области геометрии и математики в целом.
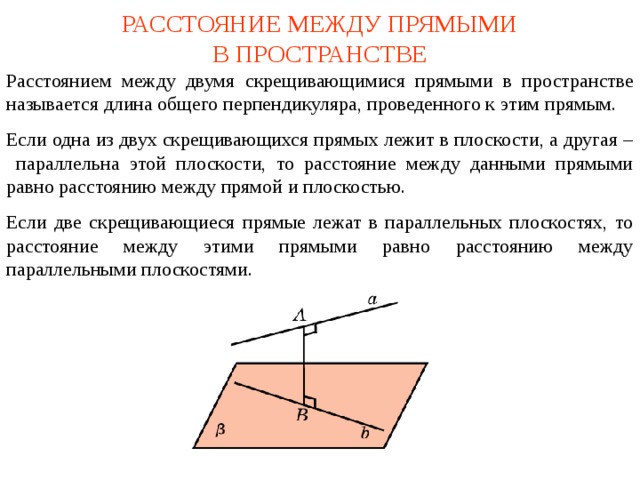
Расстояние между параллельными прямыми в пространстве
Расстояние между двумя плоскими параллельными прямыми может быть определено с помощью основной формулы для вычисления расстояния между двумя точками в трехмерном пространстве. Для этого необходимо знать координаты двух параллельных прямых.
Предположим, что у нас есть две параллельные прямые, заданные уравнениями:
l₁: Ax + By + C₁ = 0
l₂: Ax + By + C₂ = 0
где A, B — коэффициенты, C₁, C₂ — свободные члены.
Для вычисления расстояния между этими прямыми мы можем выбрать произвольную точку с координатами (x₀, y₀) на первой прямой l₁ и провести перпендикуляр из этой точки на вторую прямую l₂.
Таким образом, у нас есть две пары точек:
Точка на прямой l₁: (x₀, y₀)
Точка на прямой l₂: (x, y)
Расстояние между этими точками может быть найдено с помощью формулы:
d = √((x — x₀)² + (y — y₀)²)
Подставив координаты точек в формулу, мы сможем вычислить расстояние между параллельными прямыми.
Взаимное расположение параллельных прямых
Виды взаимного расположения параллельных прямых:
1. Расстояние между параллельными прямыми равно расстоянию между любыми двумя параллельными прямыми, перпендикулярными данным прямым. Это означает, что для определения расстояния от одной параллельной прямой к другой достаточно провести перпендикуляр из любой точки одной прямой ко второй прямой.
2. Параллельные прямые могут быть взаимно параллельными, то есть иметь одинаковое направление.
3. Параллельные прямые могут быть взаимно перпендикулярными, то есть образовывать прямой угол друг с другом.
Таблица взаимного расположения параллельных прямых:
| Вид взаимного расположения | Описание |
|---|---|
| Расстояние между параллельными прямыми | Расстояние от одной параллельной прямой до другой можно определить путем проведения перпендикуляра из любой точки одной прямой к другой |
| Взаимно параллельные прямые | Прямые, которые имеют одинаковое направление |
| Взаимно перпендикулярные прямые | Прямые, которые образуют прямой угол друг с другом |
Практическое применение расстояния между параллельными прямыми
Расстояние между двумя параллельными прямыми имеет множество практических применений в различных областях. Его использование позволяет решать реальные задачи и учитывать особенности геометрического пространства.
В архитектуре и строительстве расстояние между параллельными прямыми помогает определить ширину проходов, расстояние между стенами, высоту потолков и многое другое. Это позволяет спланировать пространство максимально эффективно и рационально.
В автотранспорте расстояние между параллельными прямыми применяется для расчета ширин и длин автомобилей, чтобы обеспечить безопасность движения на дороге. Это помогает определить, сколько места займет транспортное средство и насколько широкий должен быть проезд.
В графике и дизайне расстояние между параллельными прямыми используется для создания равномерных отступов, сеток и композиций. Это помогает улучшить визуальное восприятие и сделать изображения более сбалансированными.
Расстояние между параллельными прямыми также имеет применение в математических и физических расчетах, например, для определения пути, скорости или мощности. Оно является одним из основных элементов геометрии и используется на практике для решения конкретных задач.
В целом, понимание и использование расстояния между параллельными прямыми является важным инструментом для множества профессионалов, включая архитекторов, строителей, дизайнеров и инженеров. Оно позволяет точно измерять и учитывать пространственные параметры, что способствует более эффективной и точной реализации проектов.
Вопрос-ответ:
Что такое расстояние между двумя параллельными прямыми?
Расстояние между двумя параллельными прямыми — это длина перпендикуляра, проведенного от одной прямой до другой. Оно показывает, насколько «далеко» находятся эти прямые друг от друга и измеряется в единицах длины.
Как вычислить расстояние между двумя параллельными прямыми?
Для вычисления расстояния между двумя параллельными прямыми нужно провести перпендикуляр от одной прямой до другой. Затем измерить длину этого перпендикуляра. Это и будет расстоянием между двумя прямыми.
Чему равно расстояние между двумя параллельными прямыми?
Расстояние между двумя параллельными прямыми зависит от их положения в пространстве. Если прямые находятся на разных плоскостях, то расстояние между ними равно длине проведенного перпендикуляра. Если же прямые лежат на одной плоскости, то расстояние равно нулю, так как они не имеют пространственной разности.
Может ли расстояние между двумя параллельными прямыми быть отрицательным?
Нет, расстояние между двумя параллельными прямыми не может быть отрицательным. Оно всегда положительно или равно нулю. Если прямые пересекаются, то расстояние между ними равно нулю. Если же прямые не пересекаются, то расстояние от одной прямой до другой всегда положительно.