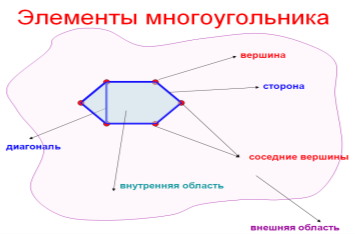
Многоугольник — это геометрическая фигура, образованная замкнутой ломаной линией, состоящей из конечного числа отрезков, называемых сторонами. Многоугольник может иметь разное количество сторон — от трех и более. В зависимости от количества сторон, многоугольники могут быть треугольниками, четырехугольниками, пятиугольниками и так далее. Слово «многоугольник» происходит от греческого префикса «много-«, означающего «много», и «угол», обозначающего точку пересечения двух линий.
Вершины многоугольника — это точки, в которых пересекаются стороны или сторона многоугольника и его продолжение. Вершины многоугольника обычно обозначаются заглавными буквами. Например, в треугольнике есть три вершины, которые обозначаются как A, B и C. Вершины многоугольника соединены отрезками — сторонами. Количество вершин в многоугольнике равно числу сторон.
Стороны многоугольника — это отрезки, соединяющие вершины многоугольника. Стороны многоугольника обозначаются строчными буквами или их комбинациями. Например, в треугольнике есть три стороны, которые обозначаются как AB, BC и CA. Стороны многоугольника имеют длину и направление. Длина сторон многоугольника может быть измерена с использованием специального инструмента — линейки или с помощью математических вычислений.
Периметр многоугольника — это сумма длин всех его сторон. Периметр многоугольника является важной характеристикой данной фигуры, так как он позволяет нам определить, насколько обширна граница этой фигуры. Для определения периметра многоугольника необходимо просуммировать длины всех его сторон. Например, периметр треугольника равен сумме длин его трех сторон.
Что такое многоугольник и как его определить?
Вершина многоугольника — это точка пересечения двух или более сторон. Вершины многоугольника обычно обозначаются большими буквами латинского алфавита, например, A, B, C и т.д.
Сторона многоугольника — это отрезок, соединяющий две соседние вершины. Стороны многоугольника обычно обозначаются маленькими буквами латинского алфавита, например, a, b, c и т.д.
Периметр многоугольника — это сумма длин всех его сторон. То есть, чтобы найти периметр многоугольника, необходимо сложить длины всех его сторон.
Определить многоугольник можно по заданным координатам его вершин. Для этого необходимо знать координаты каждой вершины и последовательность их соединения. Зная координаты вершин многоугольника, можно определить его структуру и свойства, такие как количество сторон, тип многоугольника (треугольник, четырехугольник, пятиугольник и т.д.) и периметр.
| Вершина | X-координата | Y-координата |
|---|---|---|
| A | 2 | 5 |
| B | 6 | 3 |
| C | 8 | 7 |
В приведенном примере заданы координаты вершин многоугольника. Мы можем определить, что это треугольник, так как он имеет три вершины. Чтобы найти периметр, нужно вычислить длины всех сторон и сложить их:
Длина стороны AB = √((6-2)²+(3-5)²) = √(16+4) = √20 ≈ 4.47
Длина стороны BC = √((8-6)²+(7-3)²) = √(4+16) = √20 ≈ 4.47
Длина стороны AC = √((8-2)²+(7-5)²) = √(36+4) = √40 ≈ 6.32
Периметр треугольника ABC = AB + BC + AC ≈ 4.47 + 4.47 + 6.32 ≈ 15.26
Таким образом, периметр треугольника ABC равен примерно 15.26 единицам длины.
Определение многоугольника
Многоугольник может быть простым или сложным. Простой многоугольник – это фигура, у которой нет самопересечений. Сложный многоугольник имеет пересечения сторон внутри фигуры.
Периметр многоугольника – это сумма всех его сторон. Чтобы рассчитать периметр, необходимо измерить длину каждой стороны и сложить их значения. Обычно периметр выражается в условных единицах длины, таких как сантиметры или метры.
Вершины многоугольника – это точки пересечения его сторон. Они являются конечными точками каждой стороны и обозначаются буквами латинского алфавита, например, A, B, C и т.д.
Определение многоугольника – основа для изучения различных его свойств и характеристик. Зная количество сторон и вершин, а также периметр, можно провести различные геометрические расчеты и применить их в практических задачах.
Основные характеристики
Определение многоугольника включает три основные характеристики:
- Вершины: Вершина многоугольника — это точка, где пересекаются две или более стороны. Число вершин многоугольника равно числу его сторон.
- Стороны: Сторона многоугольника — это отрезок, соединяющий две вершины. Каждая сторона может иметь разную длину.
- Периметр: Периметр многоугольника — это сумма длин всех его сторон. Он измеряется в единицах длины, таких как сантиметры или метры.
Основные характеристики многоугольника помогают определить его форму, размеры и свойства. Зная количество вершин и сторон многоугольника, можно вычислить его периметр и провести много других геометрических рассуждений.
Примеры многоугольников
Многоугольники могут иметь различное количество сторон и форму. Ниже приведены некоторые примеры многоугольников:
- Треугольник — многоугольник, состоящий из трех сторон.
- Квадрат — многоугольник, у которого все стороны равны и все углы равны 90 градусов.
- Пятиугольник — многоугольник, состоящий из пяти сторон. У него также могут быть различные комбинации углов.
- Шестиугольник — многоугольник, состоящий из шести сторон.
- Восьмиугольник — многоугольник, состоящий из восьми сторон.
Это только некоторые примеры многоугольников, существует много других форм и размеров, которыми могут обладать многоугольники. Важно помнить, что все многоугольники имеют вершины (точки, в которых стыкуются стороны) и периметр (сумму длин всех сторон).
Вершины многоугольника
Каждая вершина многоугольника обозначается буквой, например, A, B, C и т.д. Вершины многоугольника определены координатами и могут быть представлены парой чисел — абсциссой (x) и ординатой (y). Таким образом, каждая вершина имеет свои уникальные координаты.
Вершинами многоугольника можно назвать и его концевые точки, если стороны многоугольника не продолжаются за пределами этих точек. Например, в случае треугольника ABC вершинами будут точки A, B и C.
Вершины многоугольника играют важную роль при вычислении его свойств, таких как периметр и площадь. Они также определяют форму многоугольника и позволяют визуально представить его.
Пример:
Рассмотрим прямоугольник ABCD с вершинами A(0,0), B(4,0), C(4,2) и D(0,2). В этом случае вершины многоугольника образуют прямоугольник, а их координаты определены парами чисел.
Примечание: Вершины многоугольника могут быть заданы в любой последовательности, но для удобства принято задавать их по порядку обхода многоугольника по направлению против часовой стрелки.
Определение вершин
Количество вершин в многоугольнике зависит от его типа. Например, треугольник имеет три вершины, четырехугольник — четыре, пятиугольник — пять и так далее. Чем больше вершин, тем более сложный и разнообразный может быть многоугольник.
Вершины многоугольника могут быть определены как точки с заданными координатами на плоскости. Координаты вершин записываются в виде пар чисел (x, y), где x — горизонтальная координата, а y — вертикальная координата. Например, точка A с координатами (2, 3) является вершиной многоугольника.
Знание координат вершин позволяет определить расстояние между ними и вычислить периметр многоугольника. Также координаты вершин могут использоваться для построения графического представления многоугольника на плоскости.
Количество вершин
Для определения количества вершин многоугольника нужно внимательно рассмотреть его границу. Каждая точка пересечения сторон считается вершиной. Например, у треугольника три стороны и три вершины, а у пятиугольника — пять сторон и пять вершин.
Самый простой способ определить количество вершин многоугольника — посчитать их. Но если граница многоугольника сложна и численно большая, то этот способ может быть трудоемким. В таких случаях можно воспользоваться специальными формулами для определения количества вершин в зависимости от числа сторон многоугольника.
В таблице ниже представлены формулы для определения количества вершин в многоугольнике с определенным числом сторон:
| Число сторон | Количество вершин |
|---|---|
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
Таким образом, количество вершин в многоугольнике равно числу его сторон.
Стороны многоугольника
Стороны многоугольника могут иметь разную длину и направление. Например, у треугольника три стороны, а у квадрата – четыре. Длина каждой стороны может быть разной, что определяет размеры и форму многоугольника.
Стороны многоугольника могут быть прямыми или кривыми, в зависимости от формы и типа многоугольника. Например, стороны прямоугольника являются прямыми отрезками, а стороны круга – кривыми.
Периметр многоугольника равен сумме длин всех его сторон. Чтобы найти периметр, необходимо сложить длины всех отрезков, образующих многоугольник. Зная длины сторон, можно определить общую длину многоугольника и сравнить ее с другими многоугольниками.
Важно помнить, что стороны многоугольника должны быть замкнутыми, то есть каждая сторона соединяется с соседней, образуя замкнутую фигуру. Также обратите внимание на то, что стороны многоугольника должны быть непересекающимися и не иметь самопересечений.
Вопрос-ответ:
Что такое многоугольник?
Многоугольник — это двумерная геометрическая фигура, состоящая из конечного числа отрезков, называемых сторонами, которые образуют замкнутую ломаную. Все углы многоугольника являются внутренними.
Как определить вершины многоугольника?
Вершины многоугольника — это точки пересечения его сторон. Они являются конечными точками каждого отрезка, образующего многоугольник.
Как определить стороны многоугольника?
Стороны многоугольника — это отрезки, которые соединяют вершины этого многоугольника. Они образуют контур фигуры.
Что такое периметр многоугольника?
Периметр многоугольника — это сумма длин всех его сторон. Он показывает, какая длина нужна, чтобы обойти весь многоугольник по его контуру.
Как вычислить периметр многоугольника?
Для вычисления периметра многоугольника нужно сложить длины всех его сторон. Если известны координаты вершин многоугольника, можно использовать формулу расстояния между двумя точками для определения длин сторон.