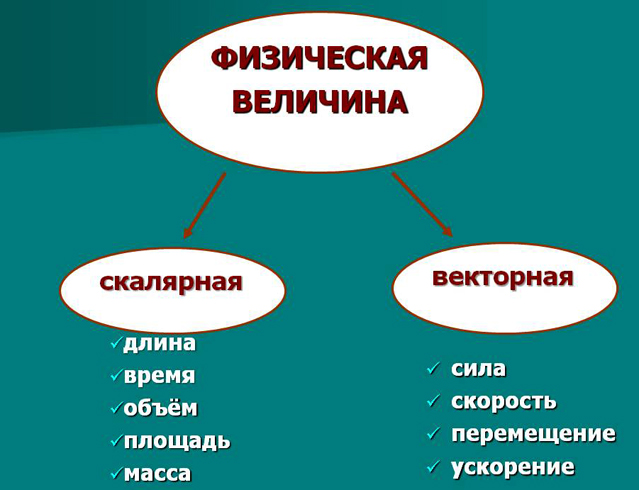
Мы живем в мире, где все вокруг нас можно измерить и описать с использованием различных физических величин. Важным понятием в физике является разделение величин на две крупные группы: векторные и скалярные.
Скалярные величины — это такие физические величины, которые полностью определяются числом и единицей измерения. Они ничего не говорят о направлении и ориентации, а лишь указывают на величину. Примерами скалярных величин могут служить масса, время, температура и давление.
В отличие от скалярных, векторные величины имеют не только величину, но и направление. Они характеризуются двумя основными свойствами: длинаю это модуль вектора, и направление. Векторные величины представлены стрелками, которые указывают на направление величины. При этом модуль вектора соответствует длине стрелки. Примерами векторных величин являются сила, скорость, ускорение и сила тяжести.
Определение и характеристики
Скалярные величины, в отличие от векторных, характеризуются только числовым значением и не имеют направления. Такие величины обозначаются обычными символами, например, масса обозначается как m. Скалярные величины могут быть положительными, отрицательными или равными нулю.
Векторы и скаляры имеют разные математические свойства. Например, скаляр можно складывать и умножать друг на друга, а векторы можно складывать и умножать только на скаляры. Также векторы подчиняются закону коммутативности — порядок слагаемых не имеет значения, а скаляры не подчиняются этому закону.
Примеры векторных величин в физике: скорость, ускорение, сила, импульс. Примеры скалярных величин: масса, объем, температура, энергия. Понимание разницы между векторными и скалярными величинами является важным для решения физических задач и построения точных моделей.
Векторные величины
Векторные величины делятся на различные виды, например:
- Положительные и отрицательные векторы. Положительные векторы имеют направление, направленное от начала координат к концу, а отрицательные – наоборот.
- Единичные векторы, которые имеют длину равную единице и используются для указания направления.
- Нулевой вектор, который имеет длину равную нулю и не указывает на какое-либо направление.
- Векторы с известными амплитудой и углом, которые указывают на направление и величину вектора.
- Сложение и вычитание векторов, которые выполняются по определенным правилам, учитывая их направления и длины.
Примерами векторных величин являются:
- Сила, которая характеризует воздействие на объект и имеет направление.
- Скорость, которая указывает на направление движения и имеет величину.
- Ускорение, которое характеризует изменение скорости и также имеет направление.
- Момент силы, который также имеет направление и указывает на вращательное действие.
- Градиент, который характеризует изменение физической величины в пространстве.
Учет направления и правильное сложение векторных величин позволяет нам адекватно описывать и предсказывать различные физические явления и процессы в нашем мире.
Скалярные величины
Скалярные величины являются основой для измерения физических величин и широко используются в научных и инженерных расчетах. Они представляют собой результат измерения, который может быть выражен в числовом значении и единицах измерения. Скалярные величины могут быть как конкретными (например, масса, объем, время), так и абстрактными (например, температура, сила, плотность).
Примеры скалярных величин:
- Масса тела: 5 кг
- Объем жидкости: 1 л
- Температура воздуха: 25 °C
- Скорость автомобиля: 60 км/ч
- Энергия: 100 Дж
Скалярные величины могут быть использованы для выполнения простых арифметических операций, таких как сложение, вычитание, умножение и деление. Они также могут быть приведены к различным системам единиц измерения для удобства использования. Например, массу можно измерять в граммах, килограммах или фунтах, а температуру — в градусах Цельсия, Кельвинах или Фаренгейтах.
Различия между векторными и скалярными величинами
В физике и математике существуют два типа величин: векторные и скалярные. Они отличаются друг от друга своими характеристиками и обладают разными свойствами.
Скалярные величины — это величины, которые полностью описываются только числовым значением и единицей измерения. Это могут быть, например, масса, время, температура, плотность и другие. Скаляры не имеют направления и не зависят от системы координат. Они могут складываться и вычитаться, умножаться и делиться друг на друга.
Векторные величины — это величины, которые не только обладают числовым значением и единицей измерения, но и имеют направление и длину. Кроме того, они зависят от системы координат. Например, это могут быть сила, скорость, ускорение, смещение и другие. Векторы могут складываться и вычитаться, умножаться и делиться на скаляры, а также выполнять другие операции.
Одним из главных отличий между векторными и скалярными величинами является то, что векторы имеют направление и могут быть представлены стрелкой на графике, а скаляры — нет. Также векторы могут быть разложены на компоненты по осям координат, а скаляры — нет.
Примером векторной величины может служить сила, которая оказывается на тело в каком-либо направлении. Примером скалярной величины может быть масса тела, которая описывает его количественную характеристику, но не имеет направления.
Векторные и скалярные величины широко применяются в различных областях науки и техники, а понимание их различий является важным для решения множества задач.
Направленность
Направление вектора определяется в пространстве с помощью нескольких параметров. Для двумерного пространства направление можно задать с помощью угла, отсчитываемого от положительного направления оси X. В трехмерном пространстве направление определяется с помощью углов от осей координат или с помощью так называемых направляющих косинусов.
Направленность вектора является одним из фундаментальных свойств, которое определяет его поведение в математических и физических задачах. Например, при выполнении операций над векторами (сложение, вычитание, умножение на число) и при решении уравнений, направление векторов играет важную роль.
В примерах использования векторных величин также активно используется их направленность. Например, при описании движения объектов или сил, векторы используются для задания направления и интенсивности этих физических величин.
| Скалярные величины | Векторные величины |
|---|---|
| Масса | Сила |
| Температура | Скорость |
| Время | Ускорение |
| Длина | Скорость |
Как видно из приведенных примеров, векторные величины обладают направленностью и позволяют задавать не только величину, но и направление интересующих нас физических величин. Без использования векторов было бы значительно сложнее и некорректнее описывать и изучать различные физические явления и процессы.
Математическое представление
В математике векторы и скаляры представляются различными обозначениями и операциями.
Скалярные величины, такие как время, масса или температура, обозначаются буквами нижнего регистра, например, t, m или T. Они описываются только одним числом и не имеют направления.
Векторные величины, такие как сила или скорость, обозначаются буквами строчными буквами с надстрочным стрелочкой, например, F или v. Они имеют как величину, так и направление.
Математически векторы представляются в виде упорядоченных пар или троек чисел, называемых компонентами вектора. В трехмерном пространстве, например, вектор скорости может быть представлен как (v₁, v₂, v₃), где каждый компонент обозначает скорость в соответствующем направлении.
Операции с векторами включают сложение и умножение на скаляр. При сложении двух или более векторов, их компоненты складываются поэлементно. Умножение вектора на скаляр также выполняется поэлементно — каждая компонента умножается на скалярное значение.
Операции
Векторные величины могут быть подвергнуты различным операциям для получения новых векторных величин или скалярных величин.
Операции над векторами:
1. Сложение векторов: Сложение двух векторов приводит к получению нового вектора, который является суммой компонентов исходных векторов.
2. Вычитание векторов: Вычитание одного вектора из другого приводит к получению нового вектора, который является разностью компонентов исходных векторов.
3. Умножение вектора на скаляр: Умножение вектора на скаляр приводит к получению нового вектора, компоненты которого являются результатом умножения компонент исходного вектора на значение скаляра.
4. Скалярное произведение: Скалярное произведение двух векторов даёт скалярную величину, которая равна сумме произведений соответствующих компонент векторов.
5. Векторное произведение: Векторное произведение двух векторов даёт вектор, перпендикулярный плоскости, образованной исходными векторами, причём этот вектор имеет величину равную площади параллелограмма, образованного исходными векторами.
Скалярные величины также могут быть подвергнуты операциям для получения новых скалярных величин или векторных величин.
Операции над скалярами:
1. Сложение скаляров: Сложение двух скалярных величин даёт новую скалярную величину, которая является суммой исходных величин.
2. Вычитание скаляров: Вычитание одного скаляра из другого даёт новую скалярную величину, которая является разностью исходных величин.
3. Умножение скаляра на скаляр: Умножение скаляра на скаляр даёт новую скалярную величину, которая является произведением исходных величин.
4. Деление скаляра на скаляр: Деление скаляра на скаляр даёт новую скалярную величину, которая является частным исходных величин.
5. Умножение скаляра на вектор: Умножение скаляра на вектор даёт новый вектор, компоненты которого равны произведению компонент исходного вектора на значение скаляра.
Примеры векторных и скалярных величин
В физике существуют два основных типа величин: векторные и скалярные. Векторные величины обладают не только числовым значением, но и направлением, тогда как скалярные величины имеют только числовое значение.
Примеры векторных величин:
| Величина | Пример |
|---|---|
| Сила | Например, сила тяжести, направленная вниз |
| Скорость | Например, скорость автомобиля, направленная вперед |
| Ускорение | Например, ускорение свободного падения, направленное вниз |
| Момент | Например, момент силы, направленный по оси вращения |
Примеры скалярных величин:
| Величина | Пример |
|---|---|
| Масса | Например, масса объекта в килограммах |
| Температура | Например, температура в градусах Цельсия |
| Время | Например, время в секундах |
| Энергия | Например, энергия в джоулях |
Знание разницы между векторными и скалярными величинами помогает в понимании физических процессов и их описании.
Примеры векторных величин
Ниже приведены примеры некоторых векторных величин:
| Название вектора | Пример |
|---|---|
| Сила | Например, сила, действующая на тело при движении или взаимодействии с другими телами, представляет собой векторную величину. Она имеет величину (измеряется в ньютонах) и направление, указывающее на то, куда действует сила. |
| Скорость | Скорость также является векторной величиной. Она указывает как быстро тело движется и в каком направлении. Например, если автомобиль едет со скоростью 50 километров в час, то скорость автомобиля — это вектор, и его направление указывает на направление движения автомобиля. |
| Ускорение | Ускорение также является векторной величиной. Оно указывает изменение скорости объекта со временем и направление этого изменения. Например, если тело движется прямолинейно и его скорость увеличивается, то ускорение будет иметь направление, указывающее на увеличение скорости. |
| Момент силы | Момент силы представляет собой векторную величину, которая определяет вращательное действие силы. Он имеет величину и направление, указывающее на ось вращения. |
Это лишь некоторые примеры векторных величин. В физике есть множество других векторных величин, которые описывают различные физические явления.
Вопрос-ответ:
Чем отличаются векторные и скалярные величины?
Векторные величины имеют не только численное значение, но и направление в пространстве, тогда как скалярные величины представляют только числовую характеристику без указания направления.
Какие примеры векторных величин можно привести?
Примерами векторных величин могут служить сила, скорость, ускорение, смещение, импульс и др.
Какие примеры скалярных величин можно привести?
Среди скалярных величин можно назвать массу, время, температуру, плотность, работу и т.д.
Какие математические операции можно выполнить с векторными величинами?
С векторными величинами можно выполнять операции сложения и вычитания, умножения на скаляр, нахождения скалярного и векторного произведения и др.
В чем практическая значимость различия между векторными и скалярными величинами?
Понимание различия между векторными и скалярными величинами необходимо для решения задач в физике, механике, геометрии и других науках, где используются физические величины и векторные операции.
Чем отличаются векторные и скалярные величины?
Векторные величины имеют не только числовое значение, но и направление, в то время как скалярные величины имеют только числовое значение. Например, скорость — векторная величина, так как помимо значения (например, 50 км/ч) она имеет определенное направление (например, северо-запад). В то же время, время — скалярная величина, так как оно имеет только числовое значение (например, 2 часа).