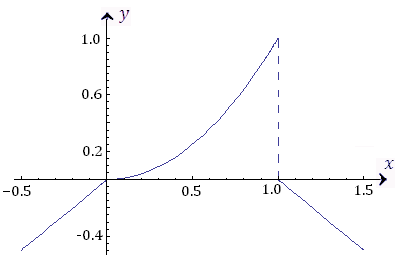
Разрыв функции в точке x0 называется разрывом первого рода если

Разрыв функции в точке x0 — это важный понятийный инструмент математического анализа. Разрыв может возникнуть в функции, когда ее значение в точке x0 не определено, или когда значение функции в этой точке определено, но отличается от значений функции на близлежащих участках. Разрыв функции может быть различных типов, и в данной статье будет рассмотрен разрыв первого рода.

Разрыв функции первого рода возникает, когда значение функции в точке x0 определено, но оно отличается от значений функции на близлежащих участках. Другими словами, существует разрыв в значении функции в точке x0, но график функции в этой точке не имеет разрыва или прерывания.

Разрыв первого рода может возникнуть, например, в случае, когда функция имеет разные пределы слева и справа от точки x0. Такой разрыв может быть вызван различными факторами, такими как наличие области неопределенности функции в точке x0 или изменение поведения функции в этой точке. Важно отметить, что разрыв первого рода может быть непрерывным в других точках своего области определения.

Содержание

Определение разрыва первого рода функции

Разрыв функции в точке \(x_0\) называется разрывом первого рода, если в этой точке значение функции не определено или существует разрыв ее значения.

Разрыв первого рода может возникнуть, если функция имеет различное значение на левой и правой сторонах точки \(x_0\) или если функция имеет бесконечное значение в этой точке.

Функция может иметь разрыв первого рода в точке \(x_0\), если она не непрерывна в этой точке, например, если она имеет устранимую разрывность, разрыв скачка или разрыв разрывность типа «1/0».

Устранимая разрывность возникает, когда значение функции можно определить в точке, за исключением этого определенного значения, путем исправления непрерывности функции в этой точке.

Разрыв скачка возникает, когда значение функции на левой и правой сторонах точки различаются, то есть предел функции в этой точке существует, но значения функции с обеих сторон отличаются и не стремятся друг к другу.

Разрывность типа «1/0» возникает, когда функция имеет бесконечное значение в точке \(x_0\), то есть предел функции в этой точке стремится к бесконечности.

Таким образом, разрыв первого рода функции может быть связан с нарушением непрерывности функции в определенной точке или с ее особыми значениями. Это понятие является важным для изучения поведения функций и их свойств.

Примеры функций с разрывом первого рода

Разрыв функции в точке \(x_0\) называется разрывом первого рода, когда значение функции в этой точке отличается от её односторонних пределов.

Ниже приведены несколько примеров функций с разрывом первого рода:

Функция	Разрыв в точке	Описание
\(f(x) = \frac{1}{x}\)	\(x = 0\)	Функция имеет вертикальную асимптоту в точке \(x = 0\), то есть её значение стремится к бесконечности при \(x\) стремящемся к 0.
\(g(x) = \text{sgn}(x)\)	\(x = 0\)	Функция меняет знак при переходе через ноль, поэтому значение в точке \(x = 0\) не может быть определено.
\(h(x) = \|x\|\)	\(x = 0\)	Функция имеет разрыв на оси \(x\) в точке \(x = 0\), так как значение функции слева и справа от нуля различается.

Эти примеры демонстрируют основные ситуации, в которых функции могут иметь разрыв первого рода.

Симметричные свойства разрыва первого рода

Симметричность значений функции

Одним из симметричных свойств разрыва первого рода является то, что значения функции в точке разрыва могут быть симметричными относительно среднего значения между границами пределов. Если значение функции на левом пределе равно A, а на правом пределе равно B, то значение функции в самой точке разрыва будет равно ((A + B) / 2). Это свойство позволяет анализировать влияние разрыва на функцию и получать более точные значения в окрестности разрыва.

Симметричность окрестности разрыва

Другим симметричным свойством разрыва первого рода является то, что окрестность разрыва также может быть симметричной относительно точки разрыва. Если левая граница предела равна x0 — a, а правая граница предела равна x0 + b, то окрестность разрыва будет представлять собой интервал (x0 — a, x0 + b), который является симметричным относительно точки разрыва. Это свойство позволяет более точно определить область изменения функции и анализировать ее поведение в окрестности разрыва.

Свойство	Описание
Симметричность значений функции	Значение функции в точке разрыва равно среднему значению между границами пределов.
Симметричность окрестности разрыва	Окрестность разрыва является симметричной относительно точки разрыва.

Графическое представление разрыва первого рода

Разрыв функции в точке x0 называется разрывом первого рода, если значение функции в этой точке не определено или не сходится к какому-либо конечному числу. Графически разрыв первого рода представляет собой разрыв в графике функции.

Если функция имеет разрыв первого рода в данной точке x0, то график функции будет иметь вид двух отдельных частей, между которыми есть некоторое расстояние:

Пример 1:

Рассмотрим функцию f(x) = 1 / x. В точке x0 = 0 функция не определена, так как невозможно делить на ноль. График функции будет иметь вид двух прямых линий, одна идет вблизи x0 с положительной стороны оси x, а вторая — с отрицательной стороны. Между ними будет пропуск, так как значение функции в точке x0 не определено.

На графике разрыв первого рода будет выглядеть как две «ломанные линии», одна из которых не примыкает к другой.

Пример 2:

Рассмотрим функцию g(x) = |x|. В точке x0 = 0 функция не сходится к конечному числу, так как значение функции в этой точке будет равно 0 для x < 0 и x > 0. График функции будет иметь вид двух частей, одна — линия y = x для x > 0, и вторая — линия y = -x для x < 0. Между ними будет существовать разрыв первого рода, так как значение функции в точке x0 не сходится к конечному числу.

На графике разрыв первого рода будет выглядеть как две линии, между которыми есть пропуск.

Таким образом, графическое представление разрыва первого рода отображает отсутствие определенного значения функции в данной точке или ее отклонение от конечного числа. Это важное свойство функций, которое позволяет анализировать их поведение и свойства в различных точках.

Причины возникновения разрыва первого рода

Разрыв функции в точке x0 называется разрывом первого рода, если значение функции в этой точке не определено или не равно ее пределу с обеих сторон.

Причины возникновения разрыва первого рода могут быть различными:

Деление на ноль. Если функция содержит выражение, в котором происходит деление на ноль в точке x0, то возникает разрыв первого рода. Например, функция f(x) = 1 / (x — 2) имеет разрыв первого рода в точке x0 = 2, так как деление на ноль неопределено.
Недопустимое значение в аргументе функции. Если функция не определена в точке x0 из-за недопустимого значения в аргументе, то возникает разрыв первого рода. Например, функция f(x) = √x имеет разрыв первого рода в точке x0 = -1, так как невозможно извлечь квадратный корень из отрицательного числа.
Скачок значений функции. Если функция имеет различные значения с обеих сторон от точки x0, то возникает разрыв первого рода. Например, функция f(x) = |x| имеет разрыв первого рода в точке x0 = 0, так как значение функции меняется с -1 на 1 при переходе через ноль.
Различные определения функции на интервалах. Если функция имеет разные определения на интервалах, содержащих точку x0, то возникает разрыв первого рода. Например, функция f(x) = 1/x имеет разрыв первого рода в точке x0 = 0, так как определена по-разному на отрицательных и положительных значениях аргумента.

Все эти причины могут привести к разрыву функции первого рода, что важно учитывать при анализе функций и их свойств.

Свойства разрыва первого рода в окрестности точки

Разрыв функции в точке x0 называется разрывом первого рода, если левосторонний предел функции отличен от правостороннего предела в точке x0.

Окрестность точки разрыва первого рода может обладать следующими свойствами:

В окрестности точки разрыва первого рода функция может быть как ограниченной, так и неограниченной.
В окрестности точки разрыва первого рода функция может быть как монотонной, так и не монотонной.
В окрестности точки разрыва первого рода функция может пересекать асимптоты или не пересекать их.
В окрестности точки разрыва первого рода функция может иметь различные виды особых точек, такие как вертикальные асимптоты или разрывы второго рода.
В окрестности точки разрыва первого рода функция может иметь несколько точек разрыва первого рода и быть непрерывной в остальных точках.

Исследование свойств разрыва первого рода в окрестности точки позволяет определить поведение функции в этой области и провести более детальный анализ ее характеристик.

Связь между непрерывностью и разрывом первого рода

Функция называется непрерывной в точке, если значение функции приближается к значению функции в этой точке, когда значение аргумента приближается к значению этой точки. Если функция не является непрерывной в точке, то возникает разрыв. Разрыв первого рода означает, что функция имеет конечное значение в точке, но может быть неопределена в этой точке.

Существует несколько способов классификации разрывов функций. Один из них — классификация по типу разрыва. Разрывы первого рода — это разрывы, при которых функция имеет конечные, но разные значения с каждой стороны точки. Например, функция может иметь разные пределы слева и справа от точки, или значение функции может быть неопределенным в точке.

Другой способ классификации — классификация по возможности удаления разрыва. Разрыв первого рода не может быть удален изменением значения функции в точке или изменением значения аргумента.

Таким образом, разрыв первого рода является результатом непрерывности функции, которая не позволяет приблизиться к значению функции в точке или изменить значение функции в этой точке.

Исследование разрывов функций и их связь с непрерывностью помогает лучше понять их свойства и поведение на различных участках определения. Это важное понятие в математике, которое применяется в различных областях, таких как анализ, физика, экономика и другие.

Практическое применение знания о разрывах первого рода

В экономике и финансовой аналитике знание о разрывах первого рода помогает в анализе рынков и финансовых инструментов. Например, при изучении графика цен акций на фондовом рынке, разрыв первого рода может указывать на значительные изменения в спросе и предложении акций, что может иметь важные последствия для инвесторов и трейдеров.

В медицине разрывы первого рода могут быть связаны с физиологическими процессами в организме. Например, знание о разрывах первого рода может помочь понять, как изменения в концентрации определенного белка влияют на функционирование клеток и органов. Это помогает в разработке лекарственных препаратов и методов лечения различных заболеваний.

Понимание разрывов первого рода также имеет практическое применение в инженерии и технике. Например, разрыв первого рода может указывать на наличие дефектов в материалах или структурах, что важно при разработке прочных и безопасных конструкций.

В общем, знание о разрывах первого рода позволяет лучше понимать и анализировать сложные системы и процессы, что играет важную роль в научных и практических исследованиях во многих областях.