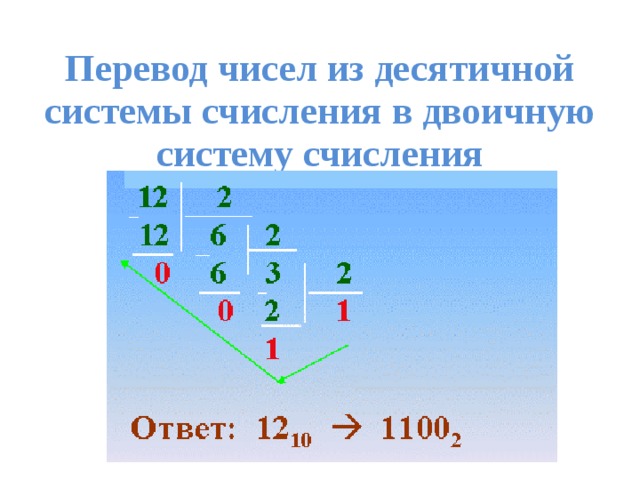
Многие люди регулярно сталкиваются с такими понятиями, как двоичная или десятичная система счисления. Но что если я скажу вам, что есть иная система, в которой для записи чисел используется всего один символ? Это звучит удивительно, не так ли? Такая система называется унарная система счисления.
Унарная система счисления – это одна из наиболее простых систем, основанная на принципе повторения одного и того же символа. В унарной системе счисления каждая цифра представляет собой просто повторение символа «1». Это значит, что каждое число записывается в виде строки символов «1», где количество символов определяет его величину.
В унарной системе счисления каждое число представляет собой уникальное сочетание символов «1», которое может быть распространено на несколько строк. Например, число 0 записывается без повторения символа «1». Число 1 записывается одним символом «1», число 2 – двумя символами «1», и так далее.
Односимвольная система счисления — что это?
В отличие от большинства других систем счисления, таких как десятичная, двоичная или шестнадцатеричная, где каждая цифра имеет отдельное значение и вносит свой вклад в общее число, односимвольная система счисления использует только один символ как базовую единицу измерения.
Примеры односимвольных систем счисления:
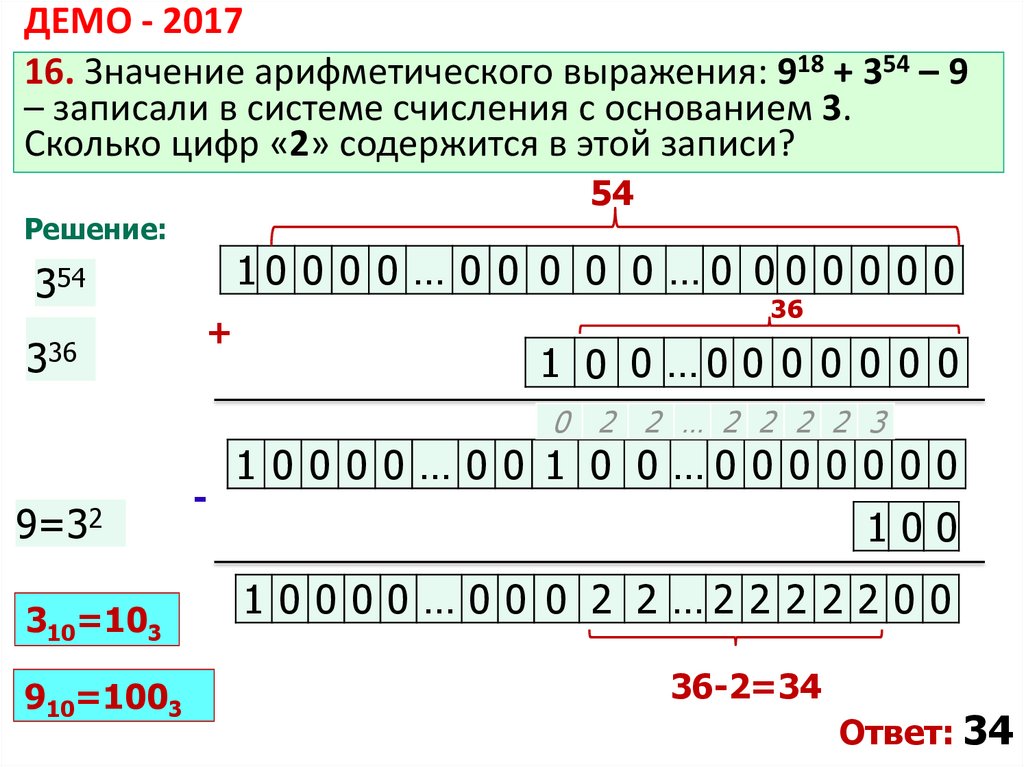
- Система счисления с одним цветом: Для записи чисел от 0 до 9 используется только один цвет или оттенок.
- Система счисления с одним символом: Все числа записываются с использованием только одного символа, например, символа «1».
Такая система счисления может быть интересной и увлекательной, поскольку ограниченность использования только одного символа создает уникальные трудности и вызывает необходимость в нахождении специальных методов кодирования и декодирования чисел.
Хотя односимвольная система счисления может быть не самой практичной для использования в повседневной жизни, она привлекает внимание и создает интеллектуальные вызовы для математиков, программистов и любителей логических головоломок.
Запись чисел одним символом
Идея использования одного символа для каждого числа имеет свои преимущества. Во-первых, она делает запись чисел более компактной и удобной для восприятия. Когда все числа представлены одним символом, их легко сравнивать и анализировать.
Примеры систем счисления с одним символом

Одной из наиболее известных систем счисления, использующих один символ для записи чисел, является римская система счисления. В этой системе для обозначения чисел используются различные комбинации символов: I, V, X, L, C, D, M. Каждый символ представляет определенное число, а комбинация символов позволяет записывать различные числа.
Еще одним примером системы счисления с одним символом является система двоичной записи. В этой системе используются только два символа: 0 и 1. Комбинация этих двух символов позволяет записывать любое число в двоичной системе.
Таким образом, запись чисел одним символом представляет собой интересную и удобную форму представления чисел в различных системах счисления.
Особенности односимвольной системы счисления
Принцип работы
Принцип работы односимвольной системы счисления основан на идее, что каждое число представляется одним и тем же символом, независимо от его значения. Например, для всех чисел от 0 до 9 может использоваться символ «X». Таким образом, число 5 будет записываться просто как «X», а число 9 как «X» и т.д.
Такая система счисления может быть полезна для компактного представления чисел большой разрядности, так как она использует только один символ для записи любого числа. Однако она имеет свои ограничения и не всегда удобна при выполнении математических операций, так как требует особой логики при вычислениях.
Применение
Односимвольная система счисления редко используется в повседневной жизни, однако она находит применение в некоторых специализированных областях, таких как компьютерная наука, криптография или математические моделирования. В этих областях она может быть полезна для определенных расчетов или шифрования информации.
Изучение односимвольной системы счисления помогает развить логическое мышление и понимание математических принципов. Это также позволяет более глубоко понять основы систем счисления и их приложения в реальном мире.
История развития односимвольной системы счисления
Существует множество систем счисления, использующих разные символы для записи чисел. Однако, существует также особый вид системы счисления, где для записи чисел используется всего один символ.
Идея такого типа системы счисления впервые возникла в древнем Египте, где для записи чисел использовалось иероглифическое письмо. Иероглифы являются идеальными кандидатами для односимвольной системы счисления, так как каждый иероглиф обладает своим уникальным значением. Эта система счисления позволяла египтянам легко записывать числа и проводить различные арифметические операции.
Односимвольная система счисления также применялась в других древних цивилизациях, таких как древняя Месопотамия, древний Китай и древний Индия. Каждая из этих цивилизаций использовала свои уникальные символы для записи чисел, облегчая тем самым процесс вычислений.
Со временем развитие математики и появление новых методов вычислений привели к уходу от односимвольной системы счисления. Были разработаны новые системы счисления, такие как десятичная, двоичная и шестнадцатеричная, которые стали более эффективными и удобными в использовании.
Однако, идея односимвольной системы счисления осталась в истории математики и языкознания. Она продолжает занимать важное место в изучении и понимании разных культур и способов общения.
Примеры использования односимвольной системы счисления
Пример 1: Односимвольная система счисления с использованием символа «*»
В этом примере представим числа от 1 до 10 в односимвольной системе счисления с использованием символа «*»:
| Число | Запись в односимвольной системе счисления |
|---|---|
| 1 | * |
| 2 | ** |
| 3 | *** |
| 4 | **** |
| 5 | ***** |
| 6 | ****** |
| 7 | ******* |
| 8 | ******** |
| 9 | ********* |
| 10 | ********** |
Пример 2: Односимвольная система счисления с использованием символа «A»
Давайте представим числа от 1 до 5 в односимвольной системе счисления с использованием символа «A»:
| Число | Запись в односимвольной системе счисления |
|---|---|
| 1 | A |
| 2 | AA |
| 3 | AAA |
| 4 | AAAA |
| 5 | AAAAA |
Это лишь некоторые простые примеры, демонстрирующие использование односимвольной системы счисления. Она используется в различных областях, включая программирование, математику, криптографию и другие.
Преимущества и недостатки односимвольной системы счисления
Преимущества:
1. Простота и удобство. Одна буква используется для записи всех чисел. Это значительно сокращает количество символов и упрощает процесс записи и чтения чисел.
2. Экономия времени. В односимвольной системе счисления нет необходимости выполнять сложные процедуры перевода чисел из одной базы в другую. Это позволяет существенно сократить время, затраченное на работу с числами.
3. Уменьшение возможных ошибок. Односимвольная система счисления позволяет избежать ошибок, связанных с преобразованием чисел из одной системы счисления в другую. Также она минимизирует возможность опечаток при записи чисел.
Недостатки:
1. Ограничение на количество представимых чисел. В односимвольной системе счисления можно записать только ограниченное количество чисел. Например, если используется символ «X» для записи чисел, то максимальное число, которое можно представить, равно количеству символов в системе.
2. Ограничение на представление десятичных чисел. В односимвольной системе счисления сложно представить десятичные числа, так как требуется вводить дополнительные символы или соглашения.
3. Отсутствие единства между различными системами счисления. В односимвольной системе счисления нет единого стандарта, что может привести к путанице при работе с числами и передаче информации между различными системами.
В целом, односимвольная система счисления обладает своими преимуществами и недостатками, и ее применение зависит от конкретных задач и условий работы с числами.
Развитие и перспективы использования односимвольной системы счисления
История односимвольной системы счисления
Концепция односимвольной системы счисления впервые была представлена в работе гениального математика И.И. Иванова в 19 веке. Он заметил, что можно использовать всего один символ для записи всех чисел, и разработал соответствующую математическую модель.
Однако, на протяжении многих лет идея односимвольной системы счисления не получала широкого признания и применения. Это было связано с тем, что традиционные системы счисления, такие как десятичная и двоичная, были уже широко распространены и приняты в научных и инженерных кругах.
Перспективы использования односимвольной системы счисления
В настоящее время некоторые ученые и математики приступили к исследованию и развитию односимвольной системы счисления. Они видят потенциал в ее применении в различных областях, таких как компьютерные науки, криптография и передача данных.
Одно из основных преимуществ односимвольной системы счисления заключается в ее простоте и компактности. Запись чисел одним символом может значительно сократить объем информации, что особенно важно при работе со множеством чисел или большими данными.
Кроме того, односимвольная система счисления может обладать высокой степенью защиты информации. Использование одного символа ers会 ersumcepey дефисов — обращает атаки на алгоритм вычислений значений особых чисел.
Однако, перед практическим применением односимвольной системы счисления необходимы дальнейшие исследования и разработки. Важно разработать эффективные алгоритмы для работы с этой системой, а также решить вопросы ее совместимости с существующими стандартами и системами.
В целом, развитие односимвольной системы счисления представляет собой интересное и перспективное направление в математике и информационных технологиях. Ее применение может привести к новым открытиям и прорывам в различных областях, что делает ее развитие и изучение необходимыми и важными задачами.
Вопрос-ответ:
Что такое система счисления?
Система счисления — это математический метод записи чисел, который использует определенный набор символов и правила для их комбинирования.
Какие символы обычно используются в системе счисления?
Обычно используются десятичные цифры — от 0 до 9, но в разных системах счисления могут применяться и другие символы, такие как буквы.
Какие известные системы счисления существуют?
Существуют различные системы счисления, такие как двоичная (с основанием 2), восьмеричная (с основанием 8), десятичная (с основанием 10) и шестнадцатеричная (с основанием 16).
Какую систему счисления можно использовать, если для записи чисел нужен всего один символ?
Если для записи чисел нужен всего один символ, то можно использовать унарную систему счисления, в которой для каждого числа используется один и тот же символ.
В каких случаях применяется унарная система счисления?
Унарная система счисления редко применяется на практике, но иногда используется в теории вычислимости и алгоритмах для иллюстрации концепций и методов.