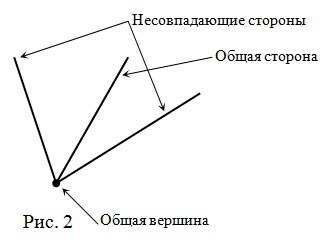
Смежные углы – это одна из основных концепций геометрии, которая позволяет нам лучше понять взаимное расположение углов и сторон. Для определения смежных углов необходимо, чтобы у них была общая сторона и внутренние углы в этой общей стороне не пересекались.
Понимание понятия смежных углов представляет собой важную базу для изучения геометрии и других математических дисциплин. Знание смежных углов помогает нам решать задачи, связанные с параллельными линиями, треугольниками и другими геометрическими фигурами.
Например: если мы имеем две параллельные линии и пересекающую их прямую, то смежные углы образуются между этими линиями и пересекающей прямой. Они имеют общую сторону и смежные углы всегда равны между собой.
Что такое смежные углы?
В геометрии два угла называются смежными, если у них есть общая сторона и они лежат на одной прямой.
Смежные углы являются основной концепцией в изучении углов и их свойств. Они позволяют анализировать и классифицировать различные углы в пространстве.
Смежные углы образуются при пересечении двух прямых. Таким образом, если на одной прямой имеется две точки A и B, а также еще одна точка C, которая лежит вне прямой AB, то угол ACB и угол ABC являются смежными.
Смежные углы могут быть как смежными дополняющими, так и смежными суплементарными:
| Смежные дополняющие углы | Смежные суплементарные углы |
|---|---|
| Два угла являются смежными дополняющими, если их сумма равна 180 градусов. | Два угла являются смежными суплементарными, если их сумма равна 90 градусов. |
| Например, углы 60 градусов и 120 градусов являются смежными дополняющими. | Например, углы 45 градусов и 45 градусов являются смежными суплементарными. |
Смежные углы имеют важное значение при решении задач на геометрию и используются в различных областях, таких как архитектура, инженерия и физика.
Смежные углы: определение и свойства
Основным свойством смежных углов является то, что их сумма равна 180 градусам. Это следует из того, что при сложении смежных углов образуется прямая, а сумма всех углов на прямой равна 180 градусам.
Есть несколько видов смежных углов, которые могут иметь дополнительные свойства:
1. Вертикальные углы: это пара углов, образованных двумя пересекающимися прямыми линиями. Вертикальные углы равны между собой, то есть их величины одинаковы.
2. Дополняющие углы: это пара углов, сумма которых равна 90 градусам. Если один угол является дополнением другого, то каждый из них называется дополняющим углом.
3. Смежно-вертикальные углы: это пара смежных и вертикальных углов. Смежно-вертикальные углы равны между собой и сумма каждой пары таких углов равна 180 градусам.
Знание определения и свойств смежных углов позволяет решать различные геометрические задачи и доказывать различные утверждения о фигурах.
Определение смежных углов
Смежные углы могут быть как прилегающими к другим углам, так и противоположными. В случае, когда они прилегают к другим углам, они образуются при пересечении двух прямых, а их вершины располагаются на одной прямой. Эти углы называются внутренними или прилегающими смежными углами.
Противоположные смежные углы образуются при пересечении двух прямых и имеют общую вершину, но находятся по разные стороны от этой вершины.
| Виды смежных углов | Описание |
|---|---|
| Внутренние смежные углы | Углы, которые прилегают к другим углам и вершины которых расположены на одной прямой. |
| Противоположные смежные углы | Углы, которые имеют общую вершину и находятся по разные стороны от этой вершины. |
Свойства смежных углов
Смежные углы обладают рядом интересных свойств, связанных с их взаимным положением и взаимодействием:
- Они расположены рядом друг с другом и имеют общую сторону.
- Сумма смежных углов всегда равна 180 градусов.
- Если один из смежных углов является прямым (равен 90 градусов), то другой смежный угол также будет прямым.
- Если один из смежных углов является остроугольным (меньше 90 градусов), то другой смежный угол будет тупоугольным (больше 90 градусов).
- Если два угла являются смежными и дополнительными (сумма их равна 180 градусов), то они являются друг другу дополнительными углами.
Изучение свойств смежных углов помогает в решении различных геометрических задач и упрощает работу с углами во многих математических расчетах.
Примеры смежных углов
В геометрии, два угла называются смежными, если они имеют общую сторону и общую вершину. Рассмотрим несколько примеров смежных углов:
- Угол КАВ и угол ВАВ – смежные углы, так как они имеют общую сторону АВ и общую вершину А;
- Угол ОАС и угол ОАВ – смежные углы, так как они имеют общую сторону ОА и общую вершину О;
- Угол ЕСА и угол ЕСВ – смежные углы, так как они имеют общую сторону ЕС и общую вершину С;
- Угол ХУВ и угол ХУГ – смежные углы, так как они имеют общую сторону ХУ и общую вершину У;
Смежные углы играют важную роль в геометрии и широко используются при решении задач.
Пример 1: углы на пересекающихся прямых
На данной диаграмме представлены прямая AB и прямая CD:
- Прямая AB:
- начальная точка — A
- конечная точка — B
- общее уравнение прямой — y = mx + b
- Прямая CD:
- начальная точка — C
- конечная точка — D
- общее уравнение прямой — y = mx + b
На пересечении прямых AB и CD образуются четыре угла:
- Угол 1: между прямыми AB и CD, обозначение — ∠ABC или ∠CBD.
- Угол 2: между прямыми AB и CD, обозначение — ∠ABD или ∠CBA.
- Угол 3: между прямыми AB и CD, обозначение — ∠BCD или ∠ADC.
- Угол 4: между прямыми AB и CD, обозначение — ∠ACD или ∠BDA.
Смежные углы указывают на то, что они имеют общую сторону. В данном случае, углы 1 и 2 являются смежными углами, потому что у них есть общая сторона AB. Также смежными являются углы 3 и 4, потому что у них есть общая сторона CD.
Пример 2: Углы при образовании параллельных линий
Рассмотрим пример, где две пары углов образованы при пересечении двух параллельных линий.
Пусть у нас есть две параллельные линии a и b. На этих линиях отметим точки A, B, C и D, расположенные в таком порядке, что A и B лежат на линии a, а C и D – на линии b:

В данном случае, угол 1 и угол 2 являются смежными, так как у них есть общая сторона AB. Они также называются смежными внутренними углами.
Угол 1 и угол 3 также являются смежными, так как у них есть общая сторона BC. Они называются смежными внешними углами.
Смежные углы при образовании параллельных линий имеют следующие свойства:
- Смежные углы сумма равна 180°
- Внутренние смежные углы при пересечении линий находятся по разные стороны от пересекающей прямой
- Внешние смежные углы при пересечении линий находятся по одну сторону от пересекающей прямой
Таким образом, понимание смежных углов при образовании параллельных линий играет важную роль в геометрии и может быть полезно в решении различных задач, связанных с этой темой.
Вопрос-ответ:
Что такое смежные углы?
Смежные углы — это два угла, которые имеют общую сторону и располагаются по обе стороны от этой стороны.
Как определить, что углы являются смежными?
Для того чтобы углы были смежными, они должны иметь общую сторону и располагаться по обе стороны от этой стороны.
Какие свойства имеют смежные углы?
Смежные углы имеют свойства: сумма мер смежных углов равна 180 градусов и смежные углы дополняют друг друга.
Зачем нужно знать о смежных углах?
Знание о смежных углах позволяет более точно анализировать и решать задачи, связанные с геометрией и измерением углов.