Что такое фигура состоящая из четырех точек и четырех отрезков

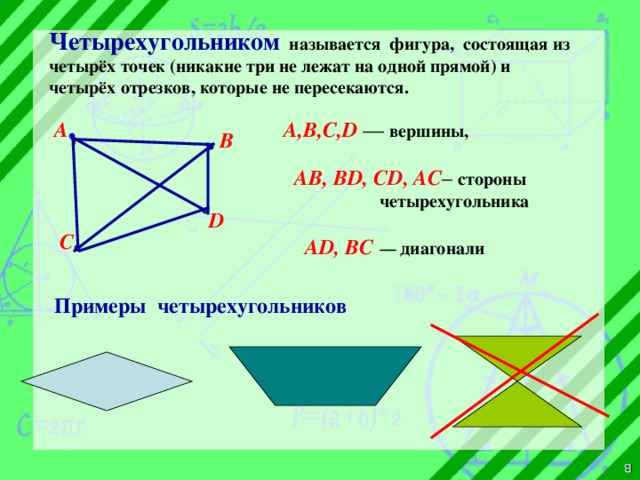
В геометрии существует множество различных фигур, каждая из которых имеет свои особенности и характеристики. Одной из таких фигур является фигура, состоящая из четырех точек и четырех отрезков.

Эта фигура называется прямоугольником. Прямоугольник – это плоская геометрическая фигура, которая имеет две параллельные стороны и противоположные углы, равные между собой. Он является основополагающим элементом при изучении геометрии, так как встречается повсеместно, от окон в домах до открытых пространств в природе.

Прямоугольники имеют множество свойств и характеристик, которые делают их интересными и полезными для решения различных задач. Один из основных параметров прямоугольника – это его площадь, которая вычисляется как произведение длины и ширины этой фигуры. Но это не единственная характеристика. Прямоугольник также имеет периметр, равный сумме длин всех его сторон, и диагонали, которые соединяют противоположные углы.

Прямоугольники находят широкое применение в различных областях науки и практики. К примеру, они используются в строительстве для создания пространств с определенными размерами и формой. Также прямоугольники применяются в графике и дизайне, где часто нужно создавать рамки, блоки и отображать информацию в упорядоченном виде.

Содержание

Фигура с четырьмя точками и отрезками: основная информация

В каждой фигуре с четырьмя точками и отрезками есть 4 вершины, которые являются конечными точками отрезков. Вершины определяют форму и размеры фигуры.

Отрезки соединяют вершины и являются сторонами фигуры. Каждый отрезок имеет начальную и конечную точки, а его длина определяет размеры каждой стороны фигуры.

Фигуры с четырьмя точками и отрезками могут иметь различные формы, такие как прямоугольник, квадрат, ромб и трапеция. Каждая из этих форм имеет свои уникальные свойства и характеристики.

Применение фигур с четырьмя точками и отрезками в различных областях включает архитектуру, инженерию, дизайн и графику. Эти фигуры часто используются для создания зданий, мебели, упаковок и различных объектов.

Таким образом, фигура с четырьмя точками и отрезками представляет собой основной элемент в геометрии, который обладает своими свойствами и может быть использован в различных областях деятельности.

Определение и основные характеристики

Фигура, состоящая из четырех точек и четырех отрезков, называется четырехугольником. Четырехугольники могут быть разного вида и обладать различными характеристиками.

Основные характеристики четырехугольника:

Стороны: Четырехугольник имеет четыре стороны, которые образуют его периметр.
Углы: Четырехугольник имеет четыре угла, которые могут быть острыми, прямыми, тупыми или разнообразными по величине.
Диагонали: Четырехугольник имеет две диагонали — отрезки, соединяющие его вершины.
Тип: В зависимости от соотношений своих сторон и углов, четырехугольники могут быть классифицированы как прямоугольники, квадраты, ромбы, параллелограммы, трапеции и др.

Четырехугольники являются важными объектами в геометрии и имеют множество свойств и особенностей, которые изучаются в математике. Их разнообразие и характеристики позволяют применять их в различных областях, например, в архитектуре, инженерии, физике и т. д.

Определение и демонстрация фигуры

Фигура, состоящая из четырех точек и четырех отрезков, называется четырехугольником. Четырехугольник имеет четыре угла и четыре стороны.

Для демонстрации четырехугольника можно использовать набор точек, соединенных отрезками. Рассмотрим пример четырехугольника, где вершины обозначены буквами A, B, C и D:

Точка A (x₁, y₁)
Точка B (x₂, y₂)
Точка C (x₃, y₃)
Точка D (x₄, y₄)

Для построения отрезков между вершинами четырехугольника, можно использовать геометрические инструменты, такие как линейка и компас. Отрезки AB, BC, CD и DA образуют стороны четырехугольника.

Четырехугольники могут иметь различные свойства и классифицироваться по типу их сторон и углов. Например, если все стороны четырехугольника равны, то он называется равнобедренным четырехугольником. Если все углы равны, то четырехугольник является квадратом.

Изучение четырехугольников позволяет лучше понять геометрию и ее применение в различных сферах, таких как архитектура, дизайн и инженерия.

Основные характеристики и параметры фигуры

Фигура, состоящая из четырех точек и четырех отрезков, имеет несколько основных характеристик и параметров, которые определяют ее форму и свойства:

Периметр: сумма длин всех сторон фигуры. Для фигуры, состоящей из четырех отрезков, периметр вычисляется путем сложения длин этих отрезков.
Площадь: мера плоской фигуры, заключенной внутри ее границ. Для фигуры, состоящей из четырех отрезков, площадь может быть вычислена различными способами, в зависимости от ее формы.
Углы: фигура, состоящая из четырех точек и четырех отрезков, имеет четыре угла. Каждый угол характеризуется своей величиной, которая измеряется в градусах.
Симметрия: некоторые фигуры, состоящие из четырех отрезков, могут обладать осевой симметрией. Осевая симметрия означает, что фигура может быть разделена на две равные части относительно оси симметрии.
Диагонали: фигура, состоящая из четырех точек и четырех отрезков, имеет две диагонали — линейные сегменты, соединяющие противоположные углы. Длина диагоналей может быть вычислена с использованием теоремы Пифагора.

Определение и изучение этих основных характеристик и параметров фигуры позволяет лучше понимать ее свойства и использовать их в различных математических и геометрических задачах.

Примеры использования фигуры в практических задачах

Фигура, состоящая из четырех точек и четырех отрезков, имеет разнообразные практические применения. Ниже приведены несколько примеров использования такой фигуры в реальной жизни.

Геометрические задачи:
- Расчет площади фигуры
- Вычисление периметра фигуры
- Определение длин отрезков, соединяющих точки фигуры
Архитектура и строительство:
- Проектирование и построение зданий с использованием трехмерных моделей, содержащих фигуры с четырьмя точками и отрезками
- Конструирование и расчет фундамента
- Размещение окон и дверей на фасаде здания
Картография:
- Построение карт с помощью географических данных и обозначение границ с использованием фигур с четырьмя точками и отрезками
- Создание специальных аннотаций и символов на карте
Дизайн:
- Создание логотипов, иконок и графических элементов
- Размещение изображений и текста на веб-страницах или в печатных материалах
- Разработка интерфейсов для программ и мобильных приложений

Это только некоторые примеры использования фигуры, состоящей из четырех точек и четырех отрезков. В современном мире существует множество практических задач, в которых такая фигура может быть полезной и необходимой.

Применение фигуры в геометрии и математике

Фигура, состоящая из четырех точек и четырех отрезков, имеет множество применений в геометрии и математике.

В геометрии, такая фигура может быть использована в качестве основы для построения других геометрических фигур. Например, с помощью такой фигуры можно построить прямоугольник или квадрат, которые являются одними из основных фигур в геометрии.

Также фигура, состоящая из четырех точек и четырех отрезков, может быть использована для решения различных математических задач. Например, она может быть использована для моделирования движения объектов или решения задач оптимизации.

В геометрии и математике, фигура, состоящая из четырех точек и четырех отрезков, также может быть использована для изучения свойств и особенностей различных геометрических объектов. Например, с помощью такой фигуры можно исследовать свойства треугольника или параллелограмма.

Примеры задач, в которых используется фигура

Фигура, состоящая из четырех точек и четырех отрезков, может быть использована в различных задачах. Вот несколько примеров:

1. Задачи геометрии:

Фигура из четырех точек и отрезков может служить основой для задач, связанных с определением площади или периметра. Например, можно рассматривать прямоугольник как фигуру, состоящую из четырех точек и четырех отрезков, и решать задачи на определение его характеристик.

2. Задачи на построение:

Фигура из четырех точек и отрезков может быть использована в задачах по построению геометрических фигур. Например, можно использовать такую фигуру в задачах на построение прямоугольника с заданными характеристиками, например, длиной одной стороны и площадью.

3. Задачи на анализ данных:

Фигура, составленная из четырех точек и отрезков, может использоваться для анализа данных. Например, можно использовать такую фигуру в задачах на исследование пространственного распределения объектов или анализ географических данных.

В общем, фигура, состоящая из четырех точек и четырех отрезков, является универсальным инструментом, который может быть применен в различных областях знаний и использован для решения разнообразных задач.

Вопрос-ответ:

Что такое фигура состоящая из четырех точек и четырех отрезков?

Фигура, состоящая из четырех точек и четырех отрезков, называется квадратом. Квадрат — это геометрическая фигура, у которой все стороны равны между собой и все углы прямые.

Можно ли рассматривать прямоугольник как фигуру, состоящую из четырех точек и четырех отрезков?

Да, прямоугольник можно рассматривать как фигуру, состоящую из четырех точек и четырех отрезков. Прямоугольник — это квадрат, у которого стороны могут быть разной длины, но при этом все углы остаются прямыми.