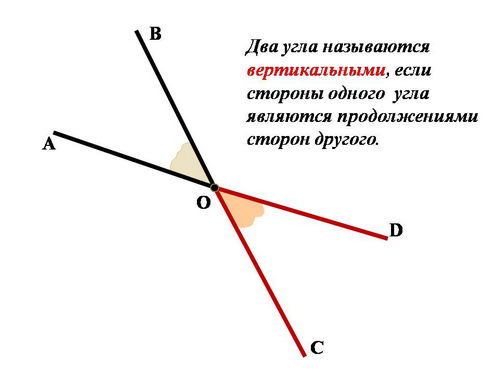
В геометрии особое внимание уделяется изучению углов, и вертикальные углы — одна из их основных разновидностей. Вертикальные углы возникают, когда два отрезка пересекаются и образуют четыре угла. Такие углы называют вертикальными, потому что они образуются при пересечении вертикальных прямых.
Вертикальные углы имеют несколько свойств, которые делают их особенными. Во-первых, они равны друг другу. Это означает, что если два угла образованы пересекающимися прямыми, то они будут иметь одинаковую величину и равны между собой. Если один из вертикальных углов имеет меру 60 градусов, то и второй угол будет равен 60 градусам.
Вертикальные углы также имеют свойство, что их сумма равна 180 градусов. Это следует из того, что вертикальные углы образуют прямую линию при пересечении прямых. Таким образом, если мы знаем меру одного из вертикальных углов, мы можем легко найти меру другого угла, вычитая из 180 градусов меру первого угла.
Свойства вертикальных углов и их названия
Свойство 1: Вертикальные углы равны друг другу. Это означает, что если два угла являются вертикальными, то они имеют одинаковую меру, то есть угол A равен углу B.
Свойство 2: Вертикальные углы дополняют друг друга. Это означает, что сумма двух вертикальных углов составляет 180 градусов. Например, если угол A составляет 60 градусов, то его вертикальный угол B составит 120 градусов, так как 60 + 120 = 180.
Из этих свойств следует ряд названий для различных комбинаций вертикальных углов:
Смежные углы: это пара углов, которые находятся рядом друг с другом и имеют общую сторону и общую вершину. Смежные углы всегда дополняют друг друга и могут быть названы как «вертикальные углы». Например, угол A и угол B являются смежными углами.
Вертикальные углы: это пара углов, которые находятся друг над другом и имеют общую вершину. Они равны и дополняют друг друга. Например, угол C и угол D являются вертикальными углами.
Изучение свойств вертикальных углов помогает в доказательстве различных геометрических теорем и решении задач, связанных с углами и их взаимодействиями.
Основные свойства вертикальных углов
Основные свойства вертикальных углов:
1. Равенство: Вертикальные углы, образованные пересекающимися прямыми, всегда равны между собой. То есть, если угол А равен углу В, то они являются вертикальными углами. Это свойство позволяет использовать равенство вертикальных углов при решении геометрических задач и построении доказательств.
2. Дополнительность: Дополнительные углы — это пары углов, сумма которых равна 180 градусов. Вертикальные углы являются дополнительными друг к другу. Если один из вертикальных углов измеряет, например, 60 градусов, то его вертикальный угол будет измерять 120 градусов. Это свойство позволяет использовать вертикальные углы для вычисления значений других углов.
3. Идентификация: Одно из основных применений вертикальных углов — идентификация независимых углов при решении геометрических задач. Если две пары углов образуют вертикальные углы, то мы можем утверждать, что они равны между собой. Это свойство позволяет нам находить значения углов и строить геометрические доказательства при решении задач.
Вертикальные углы — это важная концепция в геометрии, которая помогает нам понять и решить множество задач. Знание основных свойств вертикальных углов позволяет нам эффективно работать с ними и применять их в различных ситуациях.
Взаимное расположение
Вертикальные углы представляют собой пары углов, расположенных на противоположных сторонах пересекающихся прямых.
Взаимное расположение вертикальных углов можно определить с помощью их свойств:
| Свойство | Описание |
|---|---|
| Равенство | Если два вертикальных угла равны между собой, то каждый из них равен 90 градусам. |
| Дополняющие | Если два вертикальных угла являются дополняющими, то их сумма равна 180 градусов. |
| Смежные | Если два вертикальных угла являются смежными, то их сумма равна 90 градусов. |
Понимание взаимного расположения вертикальных углов позволяет использовать их свойства для решения геометрических задач и построения фигур.
Сумма вертикальных углов
Одно из основных свойств вертикальных углов — их сумма всегда равна 180 градусам. То есть, если имеется два вертикальных угла, то их меры всегда в сумме дают 180 градусов. Это свойство можно использовать для нахождения значения одного угла, если известна мера другого угла.
Например, если один из вертикальных углов имеет меру 40 градусов, то второй угол будет иметь меру 180 — 40 = 140 градусов. Также, если сумма двух вертикальных углов равна 180 градусам, то оба угла являются вертикальными.
Понимание свойств вертикальных углов позволяет упростить решение задач по геометрии, а также находить меру углов в простых и сложных фигурах. Знание суммы вертикальных углов также может быть полезно при изучении угловых фигур, систем углов, свойств параллельных и перпендикулярных прямых.
Названия вертикальных углов
Ниже перечислены некоторые общие названия вертикальных углов:
- Угол при вершине: это угол, который образуется двумя линиями, исходящими из одной точки.
- Угол напротив вершины: это угол, который образуется двумя линиями, пересекающимися на одной и той же прямой, но на противоположных концах.
- Угол смежный: это пара углов, образованная пересекающимися прямыми, где каждый угол находится с одной стороны пересекающей прямой, а его вершина совпадает с вершиной другого угла.
- Угол вертикально противоположный: это пара углов, образованная двумя пересекающимися прямыми, где каждый угол находится с разных сторон пересекающей прямой, а их вершины совпадают.
Знание названий вертикальных углов помогает анализировать и решать геометрические задачи, связанные с пересекающимися прямыми, истребовать углы и связи между ними.
Смежные вертикальные углы
Существуют несколько свойств, которые связаны со смежными вертикальными углами:
- Если один из смежных вертикальных углов является прямым углом, то второй угол также будет прямым, так как их сумма должна быть 180 градусов.
- Смежные вертикальные углы имеют равные меры, так как они являются дополнительными друг к другу.
- Смежные вертикальные углы могут использоваться для доказательства равенства двух углов или нахождения неизвестных углов через известные углы.
Знание свойств и названий вертикальных углов позволяет упростить геометрические задачи и решать их более эффективно. Смежные вертикальные углы являются одним из важных понятий в геометрии и широко применяются в различных областях математики и физики.
Противоположные вертикальные углы
Если две прямые пересекаются, то каждая пара противоположных вертикальных углов будет иметь одинаковую меру. Например, если один угол имеет меру 60 градусов, то его противоположный вертикальный угол также будет иметь меру 60 градусов.
Это свойство противоположных вертикальных углов может использоваться при решении задач на нахождение неизвестных углов. Если значение одного угла известно, то можно сразу определить значение его противоположного вертикального угла.
Противоположные вертикальные углы имеют такое название из-за того, что они находятся на противоположных концах пересекающихся прямых, как будто они вертикально расположены относительно друг друга.
Вопрос-ответ:
Что такое вертикальные углы?
Вертикальные углы — это пары углов, которые расположены по разные стороны пересекающихся прямых, но находятся на одной и той же высоте.
Какие свойства имеют вертикальные углы?
У вертикальных углов одинаковая мера, то есть они равны между собой.
Как найти значение вертикальных углов?
Чтобы найти значение вертикальных углов, нужно знать меру одного из них, поскольку у них одинаковая мера.
Какие еще названия используются для вертикальных углов?
Вертикальные углы также называются соответственными углами или углами, образованными параллельными прямыми.
Можно ли использовать свойства вертикальных углов для решения геометрических задач?
Да, свойства вертикальных углов широко применяются при решении геометрических задач, например, для нахождения значений неизвестных углов.
Как определить вертикальные углы?
Вертикальные углы определяются двумя пересекающимися прямыми, которые находятся на одной прямой линии и направлены в противоположные стороны.