Описанный около окружности многоугольник – это особый вид многоугольника, который обладает рядом интересных свойств. Главное из них заключается в том, что все вершины многоугольника лежат на окружности.
Из этого свойства следует, что все стороны описанного около окружности многоугольника имеют одинаковую длину. Кроме того, все углы многоугольника также равны между собой. Эти особенности делают описанный около окружности многоугольник особенно привлекательным для изучения и использования в различных областях науки и техники.
Описанные около окружности многоугольники играют важную роль в геометрии. Их свойства активно применяются при решении задач в различных областях, включая строительство, архитектуру, навигацию и даже криптографию. Понимание и умение работать с описанными около окружности многоугольниками является основой для решения множества геометрических задач.
Свойства описанного многоугольника:
1. Все вершины описанного многоугольника лежат на окружности.
2. Описанная окружность является ограничивающей для многоугольника и проходит через все его вершины.
3. Длины сторон описанного многоугольника равны радиусу описанной окружности.
4. Центр описанной окружности совпадает с точкой пересечения перпендикуляров, проведенных к серединам сторон многоугольника.
5. Углы вписанного многоугольника, образованные его сторонами и хордами, измеряют половину центрального угла, содержащего дугу между этими сторонами.
6. Сумма внутренних углов описанного многоугольника равна (n-2) * 180 градусов, где n — количество вершин многоугольника.
7. Радиус описанной окружности можно выразить через сторону многоугольника и синус половины центрального угла: R = a / (2 * sin(α/2)), где R — радиус описанной окружности, a — длина стороны многоугольника, α — центральный угол многоугольника.
Способы построения описанного многоугольника:
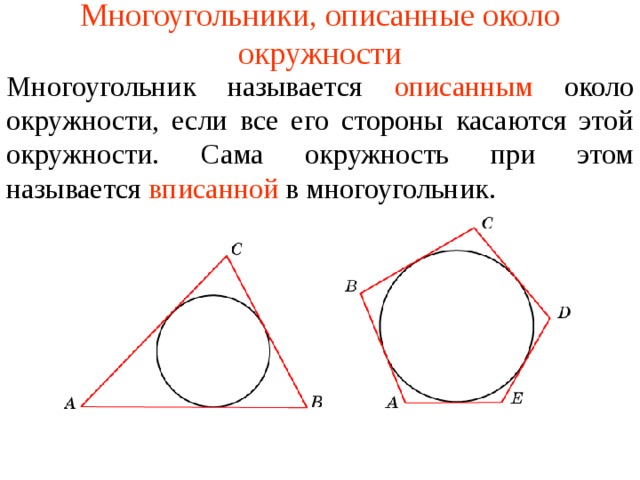
1. Способ, основанный на центральном угле:
Для построения описанного многоугольника можно использовать способ, основанный на центральном угле. Для этого необходимо:
- Найти центр описанной окружности.
- Выбрать одну из вершин многоугольника и соединить её с центром окружности.
- Разделить полученный центральный угол на количество сторон многоугольника. Это будет угол между каждой стороной многоугольника и радиусом окружности.
- Используя полученный угол, отметить точки на окружности, соответствующие вершинам многоугольника.
- Соединить полученные точки, образуя описанный многоугольник.
2. Способ, основанный на радиусе окружности:
Другим способом построения описанного многоугольника является использование радиуса описанной окружности. Для этого следует:
- Найти центр описанной окружности.
- Определить радиус этой окружности.
- Определить угол между каждой стороной многоугольника и радиусом окружности.
- Найти точку на окружности, соответствующую вершине многоугольника с помощью данного угла и радиуса.
- Соединить полученные точки, образуя описанный многоугольник.
3. Способ, основанный на перпендикуляре:
Еще одним способом построения описанного многоугольника является использование перпендикуляра. Для этого необходимо:
- Найти центр описанной окружности.
- Провести перпендикуляр к одной из сторон многоугольника из центра окружности.
- Найти точку пересечения перпендикуляра и окружности.
- Провести перпендикуляры к другим сторонам многоугольника из центра окружности.
- Найти точки пересечения перпендикуляров и окружности.
- Соединить полученные точки, образуя описанный многоугольник.
Условия, при которых многоугольник является описанным:

Многоугольник называется описанным около окружности, если все его вершины лежат на этой окружности. Описанный многоугольник обладает рядом характеристик, которые можно использовать для его определения:
1. Центр окружности:
Для описанного многоугольника существует центр окружности, вокруг которой все его вершины располагаются. Центр окружности можно найти, используя различные методы, например, с помощью пересечения перпендикуляров, проведенных к сторонам многоугольника.
2. Радиус окружности:
Радиус окружности, описанной вокруг многоугольника, равен расстоянию от центра окружности до любой его вершины. Радиус можно определить, зная координаты центра и вершины многоугольника.
3. Вписанная окружность:
Описанный многоугольник имеет вписанную окружность, которая касается всех его сторон внутренним образом. Вписанная окружность обладает свойством, что расстояния от центра окружности до всех сторон многоугольника равны.
4. Дуги и углы:
Многоугольник описывается около окружности с помощью дуг, которые соединяют его вершины. Дуги могут быть касательными или хордами. У многоугольника, который является описанным около окружности, сумма всех его внутренних углов равна 360 градусов.
Описанный многоугольник обладает множеством интересных свойств, и его свойства могут быть использованы при решении геометрических задач и конструировании фигур.
Преимущества описанного многоугольника:
1. Простота вычислений: В описанном многоугольнике, все вершины лежат на окружности, что делает его геометрические характеристики более простыми и легкими для расчета. Так, например, радиус описанной окружности может быть легко вычислен по формуле, не требуя дополнительных данных.
2. Улучшенная устойчивость: Описанный многоугольник обладает более высокой устойчивостью к деформациям и изменениям формы по сравнению с неописанными многоугольниками. Это связано с тем, что вершины описанного многоугольника находятся на окружности, что делает его конструкцию более жесткой и устойчивой.
3. Лучшая визуальная привлекательность: Описанный многоугольник обладает более симметричной и гармоничной формой, что делает его визуально привлекательным. Это особенно важно при использовании описанного многоугольника в дизайне и архитектуре, где внешний вид играет ключевую роль.
4. Больше возможностей для анализа: Описанный многоугольник предоставляет более широкий спектр информации о своих характеристиках. Например, углы, стороны и диагонали такого многоугольника могут быть проще описаны и анализированы, что позволяет более точно определить его свойства и особенности.
5. Удобство использования в вычислениях и моделировании: Описанный многоугольник имеет много практических применений в различных областях, таких как геометрия, физика и компьютерные науки. Его простота и устойчивость делают его удобным для использования в вычислениях и моделировании, а его характеристики обеспечивают точность и надежность результатов.
Примеры применения описанного многоугольника:
1. Геодезия
Описанный многоугольник наиболее часто используется в геодезии. Он позволяет определить точное положение объекта на земной поверхности с помощью триангуляции. Такой метод используется, например, при создании карт и планов местности, а также при построении геодезических сетей.
2. Компьютерная графика
В компьютерной графике описанный многоугольник используется для создания сложных форм и изображений. Он позволяет задавать точные координаты вершин и задавать линии и кривые, проходящие через эти вершины. Такой подход часто применяется при создании трехмерных моделей и анимаций.
В обоих примерах описанный многоугольник является важным инструментом для определения и создания сложных геометрических форм. Его использование позволяет достичь высокой точности и эффективности в различных областях деятельности, где требуется работать с геометрическими объектами.
Математические свойства описанного многоугольника:
Описанный многоугольник имеет ряд интересных математических свойств и особенностей, которые могут быть использованы для его анализа и решения различных задач.
1. Центр окружности:
В описанном многоугольнике существует центр окружности, которая касается всех его сторон. Центр окружности находится в точке пересечения перпендикуляров, проведенных к серединам двух сторон многоугольника.
2. Радиус окружности:
Радиус описанной окружности является постоянной величиной, которая остается неизменной для всех треугольников и многоугольников, вписанных в эту окружность.
Для многоугольника радиус описанной окружности можно найти с использованием следующей формулы:
| Количество сторон многоугольника (n) | Формула для нахождения радиуса окружности (R) |
|---|---|
| 3 (треугольник) | R = a / (2 * sin(π / 3)), где а — длина стороны треугольника |
| 4 (четырехугольник) | R = a / (2 * sin(π / 4)), где а — длина стороны четырехугольника |
| 5 (пятиугольник) | R = a / (2 * sin(π / 5)), где а — длина стороны пятиугольника |
| … | … |
Продолжая данный шаблон, можно найти радиус описанной окружности для любого многоугольника.
Таким образом, математические свойства описанного многоугольника позволяют нам более глубоко разобраться в его структуре и свойствах, а также использовать его для решения различных математических задач и задач геометрии.
Геометрическое представление описанного многоугольника:
Описанный многоугольник имеет ряд характеристических свойств:
- Все стороны описанного многоугольника равны между собой
- Все углы описанного многоугольника равны между собой
- Описанная окружность многоугольника является радиусом для всех сторон
- Центр окружности совпадает с центром многоугольника
Построение описанного многоугольника может быть выполнено с помощью геометрических методов или с использованием специализированных инструментов. Геометрическое представление описанного многоугольника позволяет легко определить его характеристики и свойства, а также использовать их в решении геометрических задач.
Вопрос-ответ:
Что такое описанный многоугольник?
Описанный многоугольник — это многоугольник, все вершины которого лежат на окружности.
Как построить описанный многоугольник?
Описанный многоугольник можно построить, проведя все диагонали внутри самого многоугольника и соединив середины полученных отрезков. Таким образом, полученный многоугольник будет описанным вокруг окружности.
Каковы свойства описанного многоугольника?
Описанный многоугольник имеет несколько свойств. Например, сумма противоположных углов описанного четырехугольника равна 180 градусов. Кроме того, сумма всех углов описанного многоугольника зависит только от его количества сторон и равна (n-2)×180 градусов.
Как связаны стороны описанного многоугольника и его радиус?
В описанном многоугольнике каждая сторона является хордой окружности, а расстояние от центра окружности до каждой стороны равно радиусу окружности.
В чем отличие описанного многоугольника от описанной окружности?
Описанный многоугольник — это многоугольник, все вершины которого лежат на окружности, в то время как описанная окружность — это окружность, которая проходит через все вершины многоугольника.
Что такое описанный многоугольник?
Описанный многоугольник — это многоугольник, все вершины которого лежат на окружности.
Какие свойства имеет описанный многоугольник?
Описанный многоугольник обладает несколькими особенностями. Во-первых, его стороны равны между собой и являются хордами окружности. Во-вторых, сумма всех внутренних углов описанного многоугольника равна (n-2) * 180 градусов, где n — количество его вершин. Кроме того, описанная окружность является центральной для многоугольника, что означает, что каждая сторона многоугольника равноудалена от центра окружности.
