
Теорема без доказательства – это феномен в математике, который вызывает удивление и интерес у ученых и простых любителей науки. Эта теорема обладает особенным свойством: она считается истинной, но в то же время ее доказательство до сих пор не было найдено или не может быть найдено.
Феномен теоремы без доказательства особенно привлекателен для математиков, так как они стремятся объяснить и понять все законы и правила этой науки. И эта теорема ставит перед ними необычайный вызов: найти доказательство для неподвластной объяснению истины.
Такие теоремы могут иметь различные повседневные названия, такие как «теорема без доказательства», «теорема без названия» или «теорема Ферма». Они обычно обозначаются в литературе как «теорема N», где N — числовое обозначение в порядке открытия.
Теоремы без доказательств: как называется главная?
В математике существует целый класс теорем, которые не требуют доказательств, их верность признается аксиоматически. Такие теоремы называются аксиомами.
Аксиомы являются основными постулатами, на которых строится определенная математическая теория. Они считаются истинными без необходимости доказывать их.
Главная аксиома, которая лежит в основе теории она не имеет фиксированного названия и может меняться в зависимости от области математики. В различных теориях она может иметь разное содержание и название.
Таким образом, каждая область математики может иметь свою главную аксиому, и ее название не является универсальным.
Например, в теории множеств главной аксиомой является аксиома выбора, которая утверждает, что для любого непустого множества можно выбрать один элемент. Во внуклассической логике главной аксиомой является закон исключённого третьего, который гласит, что для любого высказывания либо оно истинно, либо его отрицание истинно.
Таким образом, название главной аксиомы зависит от конкретной области математики и ее содержания.
Теорема неполноты Геделя
Теорема неполноты Геделя является одним из самых важных результатов в области математической логики и компьютерных наук. Она имеет широкий спектр применений, включая основы математики, теорию алгоритмов, теорию формальных языков и даже криптографию.
Формулировка теоремы
Одной из формулировок теоремы неполноты Геделя является следующая:
В каждой достаточно мощной и достаточно сложной аксиоматической системе существует пропозиция, которую невозможно доказать или опровергнуть с использованием правил и аксиом этой системы.
Иными словами, ни одна формальная система не может полностью описать свои собственные правила и аксиомы. Таким образом, всегда остаются неразрешимые или недоказуемые утверждения внутри системы.
Доказательство и последствия
Доказательство теоремы неполноты Геделя достаточно сложно и требует глубоких знаний в области математической логики. Оно основывается на использовании парадокса самоопровержения и конструкции неполного числа Геделя.
Теорема неполноты Геделя имеет ряд важных последствий для математической логики и информатики. Одним из основных последствий является негативное решение проблемы децидабильности в теории алгоритмов. Она также подрывает идею о всеобъемлющей аксиоматической системе, которая могла бы охватить всю математику и быть непротиворечивой.
| Автор | Дата |
|---|---|
| Курт Гедель | 1931 |
Теорема Безу
Теорема утверждает, что если полином P(x) делится без остатка на x-a, то значение P(a) будет равно нулю. Иными словами, a является корнем полинома P(x). Обратное также верно: если a является корнем полинома P(x), то x-a является его делителем.
Представляя полином P(x) в виде P(x) = (x-a)Q(x) + R, где Q(x) – частное, а R – остаток от деления, можно сказать, что теорема Безу утверждает, что R = 0 в случае a – корня полинома P(x).
Применение теоремы Безу может быть особенно полезным при решении задач нахождения корней полиномов и факторизации полиномиальных выражений. Также она имеет широкое применение в алгебре, теории чисел и математическом анализе.
Теорема Безу является важным инструментом в изучении алгебры и находит широкое применение в различных областях математики, позволяя эффективно исследовать свойства и поведение полиномиальных функций.
Теорема Пифагора
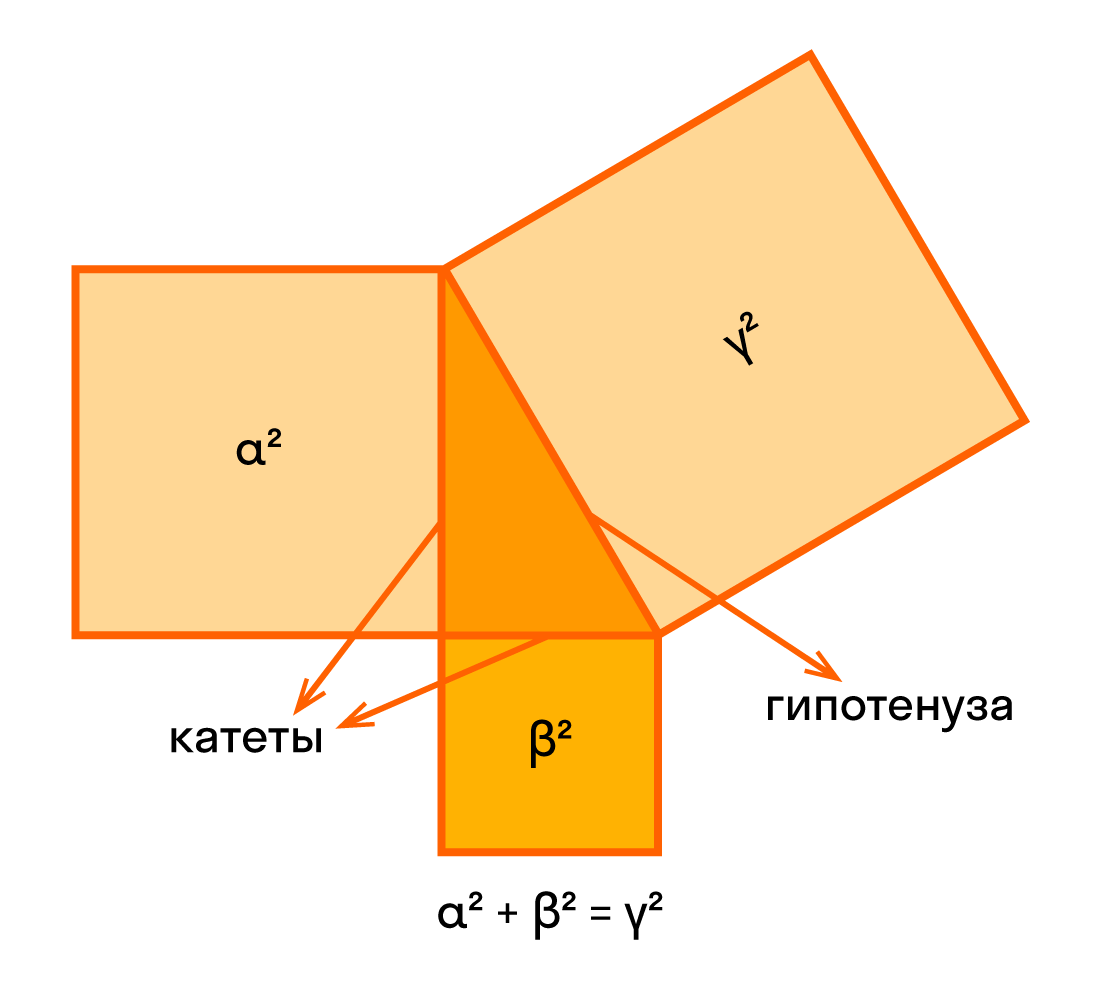
Согласно теореме Пифагора, квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. То есть, если a и b – длины катетов, а с – длина гипотенузы, то выполняется равенство:
c2 = a2 + b2
Теорема Пифагора имеет важное практическое применение и широко используется в различных областях науки и техники. Она позволяет вычислять недостающие значения сторон треугольника, а также определять, является ли данный треугольник прямоугольным.
Парадокс Банаха-Тарского
Суть парадокса заключается в том, что путем разбиения и перестановки существующего объема математики удается получить два абсолютно одинаковых объема. Иными словами, можно разбить шар на несколько частей, провести некоторые преобразования с этими частями, после чего получить два точно таких же шара, равных исходному по объему.
Парадокс Банаха-Тарского базируется на теории множеств и использует непривычные концепции, противоречащие нашему интуитивному представлению о пространстве и объеме. Для доказательства этого парадокса необходимо применить теорему выбора, которая сама не требует доказательства.
История открытия
Парадокс Банаха-Тарского был впервые представлен Стефаном Банахом в 1924 году и позднее дополнен Альфредом Тарским. Они оба были пионерами в области функционального анализа и внесли значительный вклад в развитие математической логики.
Применение парадокса
Парадокс Банаха-Тарского имеет строго теоретическое значение и не имеет применений в реальном мире. Он скорее является фундаментальным примером противоречия между интуицией и формальной логикой в математике.
| Фирма | Комплектующие |
|---|---|
| А | Шар |
| Б | Детали, способные собрать два шара по объему |
| В | Два идентичных шара |
Теорема Абеля-Руффини
Теорема Абеля-Руффини, также известная как теорема о неразрешимости общего уравнения пятой степени, гласит, что не существует общего алгебраического метода решения уравнений пятой степени с иррациональными коэффициентами. Иными словами, невозможно найти аналитическую формулу для корней уравнения пятой степени так, чтобы эта формула использовала только арифметические операции, корни, иррациональные числа и рациональные коэффициенты. Теорема Абеля-Руффини имеет важное значение в алгебре и указывает на ограничения алгебраических методов решения некоторых уравнений.
Парадокс дней рождения
Этот парадокс основан на принципе дискретности дней года и на том, что в выборке относительно небольшого числа людей количество возможных комбинаций дней рождения ограничено.
Например, в группе из 23 человек вероятность того, что двое из них имеют одинаковый день рождения, составляет более 50%. Это может показаться необычным, так как обычно мы предполагаем, что такая вероятность должна быть значительно меньше.
Однако, если внимательнее посмотреть на все возможные комбинации дней рождения в группе из 23 человек, становится понятно, что количество возможных комбинаций достаточно велико, чтобы встретиться ситуация, когда двое людей имеют одинаковый день рождения.
Парадокс дней рождения имеет важное практическое применение в теории вероятностей и статистике, и он используется для объяснения иллюзорной вероятности совпадения дней рождения в различных ситуациях, где сталкиваются большие и малые числа людей.
Теорема Ферма
Суть теоремы заключается в отсутствии таких целых чисел a, b и c, для которых выполнялось бы условие a^n + b^n = c^n, где n — целое число больше 2. Теорема Ферма была изначально сформулирована для случая n, равного 3, однако он утверждал, что у него есть доказательство для всех n, но оно слишком длинное, чтобы поместиться на полях книги.
История открытия и доказательства
Теорема Ферма стала одной из самых долгоизучаемых и неразрешенных проблем в истории математики. Более трех столетий ученые искали доказательство этой теоремы, и многие математики занимались этой проблемой в течение своей жизни.
Первый записанный доказательство был представлен британским математиком Эндрю Уайлсом в 1994 году. Однако, из-за своей сложности, его доказательство требовало использования современных методов и техник, и было проверено в течение нескольких лет. Наконец, в 1995 году, доказательство было одобрено и признано корректным, что привело к окончательному решению проблемы.
Таким образом, теорема Ферма, которая оставалась без доказательства в течение трех столетий, была наконец-то доказана благодаря усилиям Эндрю Уайлса и других математиков. Это доказательство имеет огромное значение для развития теории чисел и математики в целом.
Теорема Больцано-Вейерштрасса
Эта теорема названа в честь итальянского математика Бернардо Больцано и немецкого математика Карла Вейерштрасса.
В терминах последовательностей теорема гласит, что если последовательность ограничена, то существует такая сходящаяся подпоследовательность, которая сходится к тому же пределу, что и исходная последовательность.
Теорема Больцано-Вейерштрасса имеет множество применений и является ключевым инструментом во многих областях математики, таких как анализ, топология и функциональный анализ.
| Определение | Свойства |
|---|---|
| Пусть {an} — ограниченная последовательность. | 1. Всякая ее подпоследовательность ограничена. 2. Любая ее частичная сумма, начиная с некоторого номера, лежит в некотором ограниченном интервале. |
Вопрос-ответ:
Что такое теорема не требующая доказательств?
Теорема не требующая доказательств — это математическое утверждение, которое считается верным без необходимости предоставления формальных доказательств. Она основывается на уже известных фактах и имеет общепринятую значимость.
Какая известная теорема относится к тем, которые не требуют доказательств?
Одной из известных теорем, которая считается истинной без доказательства, является теорема Пифагора. Она утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух катетов.
В чем причина того, что некоторые теоремы не требуют доказательств?
Причина заключается в том, что эти теоремы были доказаны и проверены многократно в прошлом. Они основываются на признанных математических принципах или аксиомах, которые считаются верными.
Как эти теоремы помогают математикам?
Теоремы, которые не требуют доказательств, помогают математикам устанавливать связи между различными областями математики. Они являются важными инструментами для доказательства других теорем и развития новых математических концепций.
Какие еще примеры теорем, не нуждающихся в доказательствах, можно привести?
Кроме теоремы Пифагора, есть и другие известные теоремы, которые считаются истинными без доказательств. Например, теорема Птолемея, теорема Эйлера о гранях многогранников и многое другое.
Что такое теорема не требующая доказательств?
Теорема не требующая доказательств — это утверждение, которое считается доказанным на основе других ранее доказанных утверждений или аксиом, без необходимости проводить отдельное доказательство.