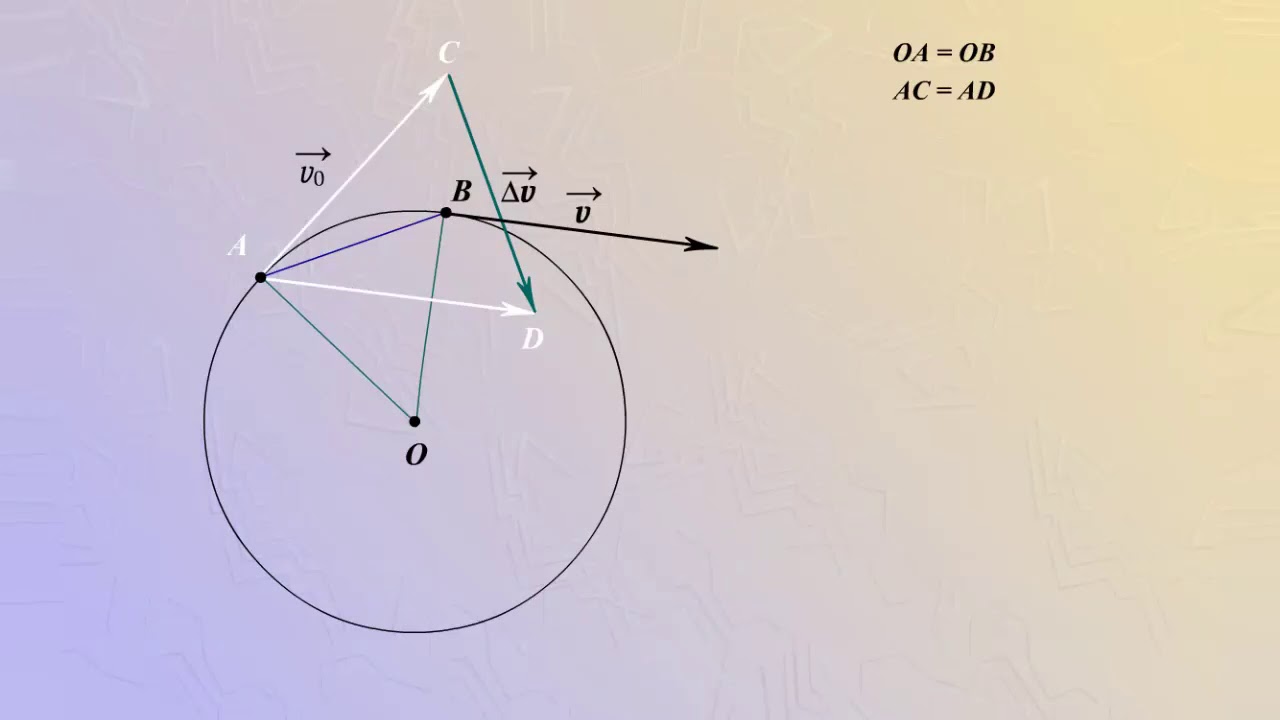
В физике равномерное движение по окружности является одним из самых простых и понятных примеров движения. Точка, движущаяся по окружности с постоянной скоростью, имеет постоянную величину и направление скорости. Однако, чтобы точка могла двигаться по окружности, необходимо действие силы, которая называется центростремительной. Эта сила направлена вдоль радиуса окружности и приводит к ускорению точки.
Ускорение точки при равномерном движении по окружности вычисляется с помощью формулы: ускорение равно квадрату скорости, деленному на радиус окружности. Таким образом, ускорение зависит от скорости движения и радиуса окружности. Чем больше скорость или радиус, тем больше ускорение.
Центростремительное ускорение является важным понятием в физике и находит применение в различных областях, включая механику и астрономию. Например, при изучении движения планет вокруг Солнца или спутников вокруг планеты необходимо учитывать центростремительное ускорение. Благодаря ему эти небесные тела остаются на своих орбитах и движутся по закону сохранения энергии.
Что такое ускорение точки на окружности?
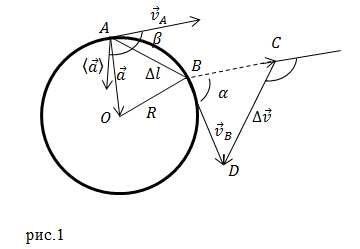
Ускорение точки на окружности связано с ее скоростью и радиусом движения. Если скорость у точки на окружности увеличивается, то ее ускорение тоже увеличивается. Также ускорение зависит от радиуса окружности: при увеличении радиуса, ускорение уменьшается, а при уменьшении радиуса, ускорение увеличивается.
Ускорение точки на окружности можно представить как результат действия двух сил: силы инерции, направленной от центра окружности, и центростремительной силы, направленной к центру окружности. В результате действия этих двух сил, точка при движении по окружности испытывает ускорение.
Формула для расчета ускорения точки на окружности:
Ускорение точки на окружности можно рассчитать с использованием следующей формулы:
a = v² / r
где:
- a — ускорение точки
- v — скорость точки
- r — радиус окружности
Таким образом, зная скорость и радиус движения точки по окружности, можно вычислить ее ускорение.
Понятие ускорения точки при равномерном движении
Ускорение точки при равномерном движении по окружности всегда направлено радиально к центру окружности и называется центростремительным ускорением. Оно обозначается символом «а» и измеряется в метрах в секунду в квадрате (м/с^2).
Значение центростремительного ускорения зависит от радиуса окружности и угловой скорости точки. Чем больше радиус окружности или угловая скорость точки, тем больше центростремительное ускорение. Формула для расчета центростремительного ускорения имеет вид:
а = R * ω^2
где «а» — центростремительное ускорение, «R» — радиус окружности, «ω» — угловая скорость точки.
Ускорение точки при равномерном движении по окружности играет важную роль в решении различных механических задач, таких как определение силы натяжения шнура, необходимой для равномерного движения точки по окружности.
Ускорение в физике: равномерное движение по окружности
Ускорение точки при ее равномерном движении по окружности называется центростремительным ускорением. Данное ускорение всегда направлено к центру окружности и имеет постоянное значение. Центростремительное ускорение можно рассчитать с помощью формулы:
aцс = v2/r
где aцс — центростремительное ускорение, v — скорость точки, r — радиус окружности.
Таким образом, чем больше скорость точки или меньше радиус окружности, тем больше центростремительное ускорение. Если радиус окружности равен нулю, то ускорение будет бесконечно большим, так как скорость точки остается постоянной.
Пример:
Пусть точка движется по окружности радиусом 2 м и имеет скорость 5 м/с. Рассчитаем центростремительное ускорение:
aцс = (5 м/с)2 / 2 м = 12.5 м/с2
Таким образом, центростремительное ускорение точки равно 12.5 м/с2.
Центростремительное ускорение играет важную роль в различных физических явлениях, таких как вращение твердого тела, движение спутников и других объектов по окружности. Познание этой концепции позволяет более точно предсказывать движение тел и проводить расчеты в различных физических задачах.
Формула для расчета ускорения точки на окружности
Ускорение точки при ее равномерном движении по окружности определяется формулой:
a = v² / R
Где:
- a — ускорение точки на окружности
- v — скорость точки на окружности
- R — радиус окружности
Эта формула выражает зависимость ускорения точки от скорости и радиуса окружности. Ускорение точки направлено к центру окружности и зависит от квадрата скорости и обратно пропорционально радиусу.
Таким образом, при увеличении скорости точки или уменьшении радиуса окружности, ускорение будет возрастать, а при уменьшении скорости точки или увеличении радиуса окружности, ускорение будет уменьшаться.
Формула для расчета ускорения точки на окружности является важным инструментом в физике и механике. Она позволяет определить, с какой силой точка движется по окружности и какие факторы влияют на ее ускорение.
Ускорение точки: зависимость от радиуса окружности
Ускорение точки при ее равномерном движении по окружности зависит от радиуса окружности, по которой она движется. Ускорение определяется как величина, изменение скорости точки по времени.
Для того чтобы понять зависимость ускорения от радиуса окружности, рассмотрим формулу для равномерного движения по окружности:
Формула равномерного движения по окружности
Скорость точки, движущейся по окружности, определяется формулой:
v = 2πr / T,
где v — скорость точки, r — радиус окружности, а T — период обращения точки по окружности.
Ускорение можно выразить как производную скорости по времени:
a = dv / dt.
Так как скорость точки постоянна, то ускорение точки при ее равномерном движении по окружности равно нулю:
a = 0.
Таким образом, при равномерном движении точки по окружности ускорение не зависит от радиуса окружности и остается равным нулю.
Ускорение точки на окружности: примеры из повседневной жизни
Ускорение точки при ее равномерном движении по окружности называют центростремительным ускорением. Оно всегда направлено к центру окружности и определяется по формуле:
ac = v2/r
где ac — центростремительное ускорение, v — скорость движения точки, r — радиус окружности.
Центростремительное ускорение играет важную роль во многих сферах нашей жизни. Рассмотрим несколько примеров, где оно проявляется:
| Пример | Описание |
|---|---|
| Аттракционы в парке развлечений | Во многих аттракционах, таких как колесо обозрения или карусель, центростремительное ускорение создает ощущение скорости и веселья у посетителей. |
| Круговое движение автомобиля на повороте | При движении автомобиля по круговому повороту, центростремительное ускорение позволяет машине сохранять равномерное движение и не вылетать из поворота. |
| Катание на велосипеде по кругу | При катании на велосипеде по кругу, центростремительное ускорение позволяет райдеру сохранять равновесие и не упасть во время прохождения поворотов. |
Это лишь некоторые примеры, где центростремительное ускорение играет важную роль. От его величины зависит комфорт и безопасность многих видов движения.
Зависимость ускорения точки от периода вращения
Ускорение точки при ее равномерном движении по окружности зависит от периода вращения и равно произведению квадрата скорости и радиуса окружности, деленного на радиус возможно нахождения точки:
Формула:
Ускорение = (Скорость² * Радиус) / Радиус возможного нахождения точки
Радиус возможного нахождения точки — это расстояние от точки до оси вращения.
Таким образом, чем больше период вращения, тем больше ускорение точки при ее равномерном движении по окружности. Если радиус возможного нахождения точки равен радиусу окружности, то ускорение будет максимальным. Если радиус возможного нахождения точки равен нулю, то ускорение будет равно нулю.
Из данной зависимости следует, что ускорение точки может быть изменено путем изменения скорости, радиуса окружности или радиуса возможного нахождения точки.
Ускорение точки: отличие от радиального ускорения
Ускорение точки при ее равномерном движении по окружности называют центростремительным ускорением. Это ускорение направлено к центру окружности и зависит от радиуса окружности и скорости точки.
Однако, не следует путать центростремительное ускорение с радиальным ускорением. Радиальное ускорение определяет скорость изменения направления движения точки на окружности.
Центростремительное ускорение
Центростремительное ускорение, обозначаемое как aцс, является векторной величиной и всегда направлено к центру окружности.
Центростремительное ускорение можно выразить формулой:
aцс = v2/r
где v — скорость точки, r — радиус окружности.
Радиальное ускорение
Радиальное ускорение, обозначаемое как aр, также является векторной величиной и определяет изменение направления движения точки на окружности.
Радиальное ускорение можно выразить формулой:
aр = v2/r
где v — скорость точки, r — радиус окружности.
Однако, в отличие от центростремительного ускорения, радиальное ускорение может быть направлено как к центру окружности, так и от него, в зависимости от изменения направления движения точки.
Таким образом, хотя центростремительное и радиальное ускорение связаны между собой, они имеют разное направление и выполняют разные функции в равномерном движении по окружности.
Применение ускорения точки на окружности в инженерии
Ускорение точки при ее равномерном движении по окружности играет важную роль в инженерии. Это связано с тем, что ускорение позволяет определить динамику объекта и его способность изменять скорость движения.
Одним из применений ускорения точки на окружности является проектирование приводных систем, которые используются в многих машинах и механизмах. Ускорение точки необходимо учитывать при разработке системы передачи движения для определения необходимой мощности и прочности деталей.
Еще одним применением ускорения точки на окружности является проектирование транспортных средств. Например, при разработке автомобилей ускорение точки позволяет определить динамику транспортного средства при поворотах и изменении скорости. Это позволяет улучшить безопасность и управляемость автомобиля.
В области робототехники ускорение точки на окружности также имеет применение. При программировании роботов необходимо учесть ускорение точки для определения траекторий движения и скорости работы роботов. Это позволяет роботам эффективно выполнять задачи и избегать столкновений.
Таким образом, ускорение точки при ее равномерном движении по окружности играет важную роль в различных областях инженерии. Оно позволяет определить динамику объектов и разрабатывать более эффективные и безопасные технические решения.
Вопрос-ответ:
Что такое ускорение точки при ее равномерном движении по окружности?
Ускорение точки при ее равномерном движении по окружности называют центростремительным ускорением. Оно всегда направлено к центру окружности и является постоянным по величине.
Как определить величину ускорения точки при ее равномерном движении?
Величину ускорения точки при ее равномерном движении по окружности можно определить с помощью формулы a = v^2 / R, где a — ускорение, v — скорость точки, R — радиус окружности.
Какое значение имеет ускорение точки при равномерном движении по окружности, если скорость равна нулю?
Если скорость точки при ее равномерном движении по окружности равна нулю, то ускорение также будет равно нулю, так как ускорение зависит от квадрата скорости.
В каком направлении действует ускорение точки при равномерном движении по окружности?
Ускорение точки при ее равномерном движении по окружности всегда направлено к центру окружности. Это особенность центростремительного ускорения, которое служит для сохранения точки на окружности.
Может ли ускорение точки при равномерном движении по окружности меняться со временем?
Ускорение точки при равномерном движении по окружности не изменяется со временем, так как скорость точки остается постоянной. Оно всегда будет постоянным по величине и направленным к центру окружности.
Какое ускорение имеет точка при ее равномерном движении по окружности?
При равномерном движении точки по окружности её ускорение равно нулю. Ускорение точки определяется как изменение её скорости на единицу времени. В случае равномерного движения скорость точки постоянна и не изменяется, следовательно, ускорение равно нулю.
Что означает ускорение точки при ее равномерном движении по окружности?
Ускорение точки при равномерном движении по окружности означает, что ее скорость не изменяется со временем, но ее направление постоянно меняется. Такое ускорение называется центростремительным ускорением и всегда направлено к центру окружности. Его величина определяется по формуле a = v^2/R, где v — скорость точки, R — радиус окружности.