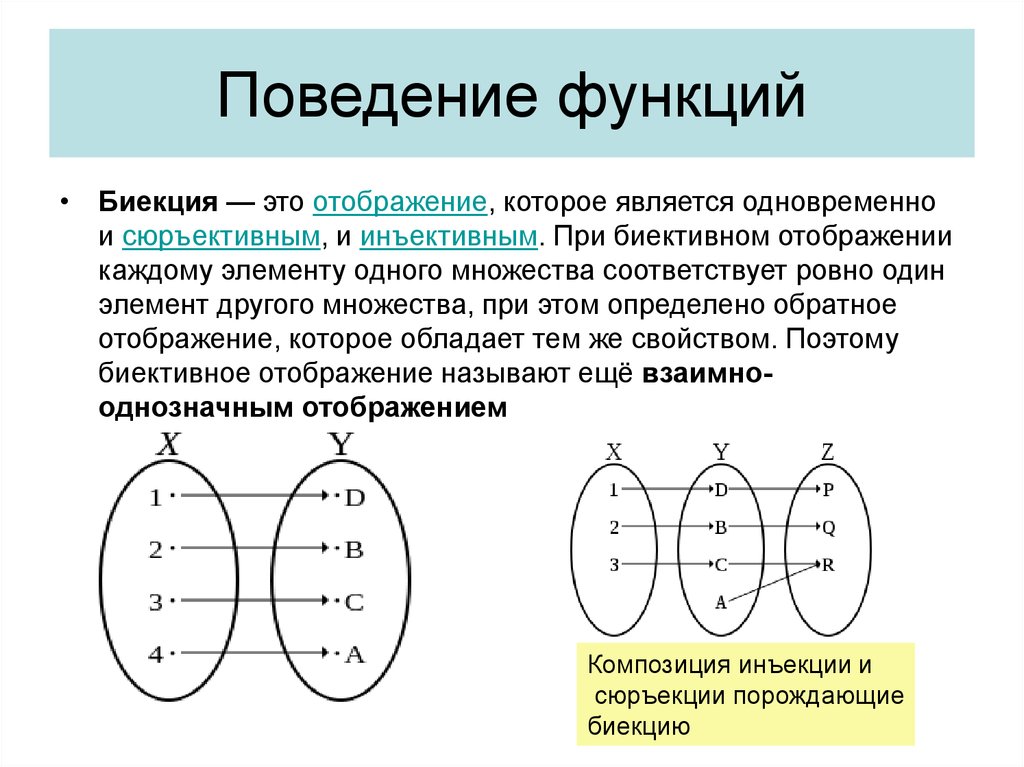
В математике взаимно однозначное отображение является специальным типом отношения между элементами двух множеств. Оно обладает свойством, что каждому элементу из одного множества соответствует ровно один элемент из другого множества, и наоборот.
Формально, отображение множества х на множество у называется взаимно однозначным, если для любых двух элементов x1 и x2 из х (x1 ≠ x2) существуют их образы y1 и y2 из у, такие что f(x1) = y1 и f(x2) = y2, причем y1 ≠ y2.
Взаимно однозначное отображение также называется биекцией или инъективным отображением. Оно является одним из основных понятий в теории множеств и имеет важные приложения в различных областях математики и информатики.
Определение взаимно однозначного отображения
Для формального определения взаимно однозначного отображения множества х на множество у, необходимо проверить выполнение двух условий:
- Инъективность: каждый элемент из множества х имеет свой уникальный образ в множестве у. Если элементы х и х’ различны, то их отображения на элементы у и у’ также должны быть различны: f(х) ≠ f(х’).
- Сюръективность: каждый элемент из множества у имеет свой прообраз в множестве х. Это означает, что для любого элемента у из множества у существует такой элемент х из множества х, что f(х) = у.
Если отображение удовлетворяет обоим условиям, то оно является взаимно однозначным.
Пример
Рассмотрим множество х = {1, 2, 3} и множество у = {a, b, c}. Определим отображение f: х → у следующим образом: f(1) = a, f(2) = b, f(3) = c. В данном случае, каждому элементу из множества х соответствует ровно один элемент из множества у, и наоборот, поэтому отображение f является взаимно однозначным.
Однако, если мы определим отображение g: х → у следующим образом: g(1) = a, g(2) = a, g(3) = c, то это отображение уже не будет взаимно однозначным, так как элементу 2 из х соответствуют два различных элемента a и b из у.
Отображение без повторений
Отображение без повторений имеет важное значение в математике и науке. Оно позволяет установить однозначное соответствие между элементами двух разных множеств, что помогает в решении различных задач и анализе данных. Например, отображение без повторений может использоваться для построения биекции между множеством натуральных чисел и множеством целых чисел.
Отображение без повторений также называется инъективным отображением или инъекцией. Этот термин происходит от латинского слова «injectio», что означает «впрыскивание». Инъекция, как и отображение без повторений, «впрыскивает» элементы одного множества в элементы другого множества без потери информации.
Для определения отображения без повторений необходимо проверить, что каждому элементу х из множества х соответствует только один элемент у из множества у, и наоборот. То есть, если a и b — различные элементы множества х, то f(a) и f(b) — должны быть различными элементами множества у, и наоборот.
Отображение без повторений играет важную роль в доказательствах и алгоритмах. Оно позволяет строить соответствия и устанавливать связи между элементами разных множеств, что открывает новые возможности и способы решения задач в различных областях науки и техники.
Отображение с полным охватом
То есть, если x и y являются элементами соответствующих множеств, то отображение f таково, что для каждого x существует единственный y, и для каждого y существует единственный x такой, что f(x) = y и f(y) = x.
Отображение с полным охватом является важным понятием в теории множеств и дискретной математике. Оно играет важную роль в решении различных задач, таких как криптография, комбинаторика, алгоритмы и т.д.
Примером отображения с полным охватом может служить отображение множества натуральных чисел на множество четных чисел. Каждому натуральному числу можно сопоставить уникальное четное число, и наоборот.
Отображение с обратимостью

Отображение множества X на множество Y называется взаимно однозначным отображением (или биекцией), если каждому элементу x из X соответствует уникальный элемент y из Y, и наоборот: каждому элементу y из Y соответствует уникальный элемент x из X. Обратимость означает, что существует взаимно однозначное отображение, которое отображает множество Y на множество X. Таким образом, отображение с обратимостью устанавливает биективную связь между элементами двух множеств.
Отображение биективное
Иными словами, биективное отображение отображает каждый элемент х на элемент у без потери информации. Это значит, что каждому элементу х соответствует только один элемент у, и наоборот, каждому элементу у соответствует только один элемент х.
Биективное отображение является взаимно обратным и имеет обратное отображение, которое также является биективным. Эти свойства делают биективное отображение особенно полезным и интересным в математике и различных областях приложений.
| Множество х | Множество у |
|---|---|
| элемент х1 | элемент у1 |
| элемент х2 | элемент у2 |
| элемент х3 | элемент у3 |
В таблице представлен пример биективного отображения между множеством х и множеством у. Каждому элементу х соответствует уникальный элемент у, и наоборот.
Отображение инъективное
Свойства отображения инъективного:
- Каждый элемент х имеет уникальное соответствие в множестве у.
- Два разных элемента х и х’ из множества х не могут иметь одинаковое соответствие в множестве у.
- Если элемент у принадлежит образу отображения, то существует только один элемент х, который ему соответствует.
- Необязательно все элементы множества у должны иметь соответствие в множестве х.
Пример:
Рассмотрим отображение множества х = {1, 2, 3} на множество у = {a, b, c}.
Если мы определяем отображение следующим образом: f(1) = a, f(2) = b, f(3) = c, то это отображение является инъективным.
При этом каждому элементу х из множества х соответствует только один элемент у, и каждый элемент у из множества у имеет соответствие в множестве х.
Отображение инъективное может быть полезно, когда нам необходимо установить взаимно однозначное соответствие между элементами двух множеств.
Замечание: Отображения инъективные являются частным случаем биективных отображений, при которых каждый элемент х из множества х имеет соответствие в множестве у, и каждый элемент у из множества у имеет соответствие в множестве х.
Отображение сюръективное
Отображение сюръективное также называется «отображением на» или «сюръекцией». Чтобы отображение было сюръективным, каждому элементу множества Y должен соответствовать хотя бы один элемент множества X.
Сюръективное отображение является частным случаем отображения, при котором каждому элементу множества Y может соответствовать несколько элементов множества X. В этом случае отображение называется многозначным.
Примеры сюръективных отображений:
1. Отображение f: X -> Y, где X = {1, 2, 3} и Y = {a, b, c}, заданное правилом f(1) = a, f(2) = b, f(3) = c.
2. Отображение g: Z -> N, где Z — множество целых чисел, а N — множество натуральных чисел, заданное правилом g(x) = |x|.
Важно!
Сюръективное отображение должно удовлетворять условию, что для каждого элемента y из множества Y существует хотя бы один элемент x из множества X, такой что f(x) = y. Если существует элемент y из множества Y, для которого не существует соответствующего ему элемента x из множества X, отображение не будет сюръективным.
Важность взаимно однозначных отображений
Взаимно однозначные отображения имеют множество полезных свойств и применений. Одним из наиболее важных является возможность использования их для определения равномощности множеств. Если существует взаимно однозначное отображение между двумя множествами, то эти множества имеют одинаковую мощность и называются равномощными. Это позволяет сравнивать множества и устанавливать их размерность.
Взаимно однозначные отображения также имеют применение в областях, связанных с криптографией и информационной безопасностью. Они используются для создания шифров и защиты информации. Важным аспектом в этом случае является то, что взаимно однозначное отображение гарантирует, что никакая информация не потеряется или будет переведена неправильно при шифровании и расшифровании данных.
Взаимно однозначные отображения также играют важную роль в теории функций и алгебре. Они позволяют формализовать различные математические концепции и связи между ними, а также устанавливать свойства функций, такие как инъективность и сюръективность.
Таким образом, взаимно однозначные отображения являются важным инструментом в математике и других научных дисциплинах. Они позволяют устанавливать связи между множествами, определять равномощность, защищать информацию и формализовать математические концепции.
Вопрос-ответ:
Что такое взаимно однозначное отображение множества х на множество у?
Взаимно однозначное отображение множества х на множество у (или биекция) — это такое отображение, которое обладает свойствами инъективности и сюръективности. Иными словами, каждому элементу множества х соответствует ровно один элемент множества у, и каждый элемент множества у имеет соответствующий ему элемент множества х.
Чем отличается взаимно однозначное отображение от обычного отображения?
Взаимно однозначное отображение (биекция) отличается от обычного отображения тем, что оно должно быть одновременно инъективным и сюръективным. Инъективность означает, что каждому элементу множества х соответствует ровно один элемент множества у, а сюръективность означает, что каждый элемент множества у имеет соответствующий ему элемент множества х.
Как можно доказать, что отображение является взаимно однозначным?
Для доказательства того, что отображение является взаимно однозначным, необходимо и достаточно показать, что оно является одновременно инъективным и сюръективным. То есть, нужно доказать, что каждому элементу множества х соответствует ровно один элемент множества у, и каждый элемент множества у имеет соответствующий ему элемент множества х. Это может быть сделано с помощью математических операций и логических рассуждений.
Зачем нужны взаимно однозначные отображения между множествами?
Взаимно однозначные отображения между множествами имеют важное значение в математике и других областях науки. Они позволяют установить взаимно однозначное соответствие между элементами двух множеств и использовать это соответствие для решения различных задач. Например, взаимно однозначные отображения используются для разработки алгоритмов шифрования данных, построения биективных связей между различными информационными структурами и многое другое.