Отрезок – это одна из фундаментальных геометрических фигур, которая представляет собой часть прямой между двумя точками. В геометрии отрезок обозначается двумя конечными точками, в которых он заканчивается.
Центр окружности – это точка, которая равноудалена от всех точек окружности. Окружность можно представить как множество всех точек в плоскости, удаленных на одно и то же расстояние от центра.
Отрезок, соединяющий центр окружности с любой ее точкой, называется радиусом. Радиус является важным понятием в геометрии и находит свое применение в различных математических и физических задачах. Радиус является одной из основных характеристик окружности.
Соединение центра окружности и ее точки радиусом образует прямую линию, которая имеет определенные свойства и характеристики. Например, радиус является самым коротким отрезком, соединяющим центр окружности и ее точку. Также радиус является радиус-вектором вектора, направленного от центра окружности к ее точке.
Отрезок соединяющий центр окружности с точкой
В геометрии радиус является важной характеристикой окружности. Он определяет ее размер и форму. Радиус также используется для вычисления других характеристик окружности, таких как длина окружности и площадь круга.
Чтобы найти радиус окружности, можно воспользоваться формулой:
- R = √(x2 — x1)2 + (y2 — y1)2
где (x1, y1) — координаты центра окружности, а (x2, y2) — координаты точки на окружности.
Радиус окружности также можно найти, зная диаметр окружности. Диаметр — это отрезок, проходящий через центр окружности и имеющий концы на границе окружности. Диаметр обозначается символом D.
Связь между радиусом и диаметром выражается следующей формулой:
- D = 2R
Это означает, что диаметр окружности в два раза больше радиуса.
Использование радиуса позволяет удобно описывать и анализировать геометрические свойства окружностей. Радиус является ключевым понятием в геометрии и находит применение во многих разделах науки и техники.
Определение отрезка, соединяющего центр окружности с точкой
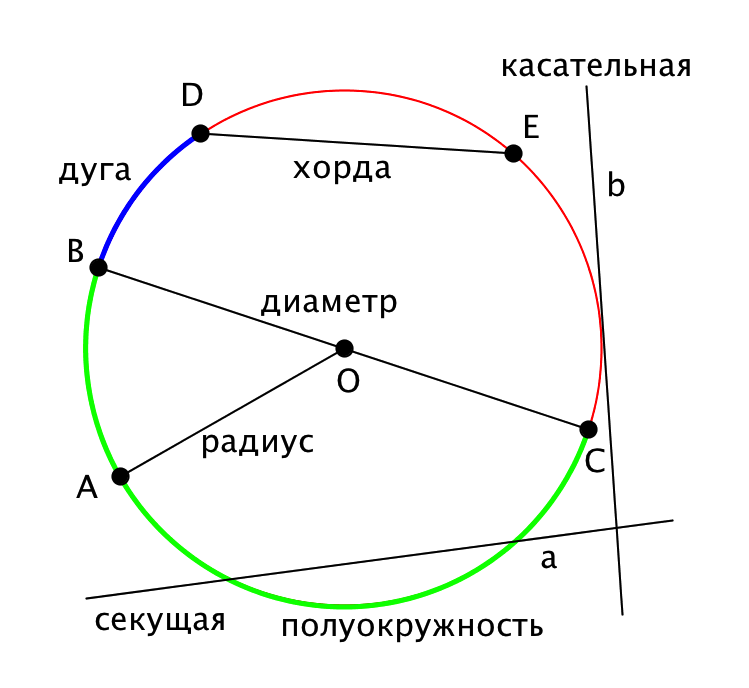
В геометрии, центр окружности обозначается буквой O. Пусть P — произвольная точка на окружности.
Тогда отрезок OP — это отрезок, который соединяет центр окружности с точкой P.
Особенностью отрезка OP является то, что он равен радиусу окружности. Радиус окружности обозначается буквой r.
Таким образом, длина отрезка OP равна r.
Отрезок, соединяющий центр окружности с точкой, имеет важное значение при решении задач геометрии. Например, при нахождении длины дуги окружности или при определении угла между двумя радиусами, проходящими через точки на окружности.
Свойства отрезка, соединяющего центр окружности с точкой
Отрезок, соединяющий центр окружности с любой ее точкой, обладает рядом интересных свойств:
- Длина этого отрезка равна радиусу окружности.
- Такой отрезок является диаметром окружности.
- Центр окружности является серединой этого отрезка.
- Все отрезки, соединяющие центр окружности с точками на окружности, имеют одинаковую длину.
- Отрезок, соединяющий центр окружности с точкой на окружности, перпендикулярен к этой точке и касательной к окружности в данной точке.
- Такой отрезок разделяет окружность на две равные дуги.
- Угол между двумя такими отрезками в центре окружности равен 180 градусов.
Такие свойства отрезка, соединяющего центр окружности с точкой, позволяют использовать его для решения различных геометрических задач и определения других характеристик окружности.
Формула вычисления длины отрезка, соединяющего центр окружности с точкой
Пусть координаты центра окружности равны (x0, y0), а координаты точки равны (x1, y1). Тогда расстояние d между центром окружности и точкой можно вычислить по следующей формуле:
d = √((x1 — x0)² + (y1 — y0)²)
Таким образом, чтобы найти длину отрезка, соединяющего центр окружности с точкой, необходимо знать координаты центра и точки, и подставить их в формулу.
Примеры использования отрезка, соединяющего центр окружности с точкой
Отрезок, соединяющий центр окружности с точкой, имеет особое значение и широкое применение в геометрии. Рассмотрим несколько примеров использования данного отрезка.
Пример 1: Нахождение радиуса окружности
Для нахождения радиуса окружности можно использовать отрезок, соединяющий центр окружности с одной из ее точек. Зная длину этого отрезка и зная, что он равен радиусу, можно легко определить радиус окружности.
Пример 2: Вычисление площади сектора
Сектор окружности — это фигура, ограниченная дугой окружности и двумя радиусами, один из которых является отрезком, соединяющим центр окружности с точкой на дуге. Для вычисления площади сектора необходимо знать радиус и длину отрезка, соединяющего центр с точкой на дуге.
Таким образом, отрезок, соединяющий центр окружности с точкой, играет важную роль в определении характеристик окружности и дает дополнительные возможности для проведения геометрических вычислений.
| Пример | Описание |
|---|---|
| Пример 1 | Нахождение радиуса окружности |
| Пример 2 | Вычисление площади сектора |
Применение отрезка, соединяющего центр окружности с точкой в математике
В геометрии, отрезок, соединяющий центр окружности с ее точкой, называется радиусом. Радиус является важным понятием в окружностях и имеет ряд свойств, которые используются при решении различных задач.
Применение отрезка, соединяющего центр окружности с точкой, включает:
- Вычисление длины радиуса. Радиус является определяющим параметром окружности и используется при вычислении длины окружности, площади окружности и других характеристик.
- Определение положения точек на окружности. Радиус позволяет определить, находится ли точка на окружности, внутри или снаружи нее. Это свойство используется, например, при построении графиков кривых и окружностей.
- Доказательство теорем. Отрезок, соединяющий центр окружности с точкой, может быть использован в доказательствах различных теорем о свойствах окружностей и их отношениях с другими геометрическими фигурами.
- Определение радиуса по его свойствам. Используя информацию о других характеристиках окружности, таких как площадь, длина окружности и другие, радиус может быть вычислен в соответствии со специфическими формулами и теоремами.
Одним из основных применений отрезка, соединяющего центр окружности с точкой, является использование его свойств при решении задач геометрии, строительства и научных исследований. Понимание и умение применять эти свойства является необходимым для успешного владения математикой в области геометрии и аналитической геометрии.
Применение отрезка, соединяющего центр окружности с точкой в физике
В механике этот отрезок используется для определения радиуса окружности и анализа ее движения. Радиус окружности, определенный через отрезок, связывает геометрические характеристики окружности и физические параметры объекта. Также данный отрезок является основой для определения момента инерции и механической энергии точечного объекта, движущегося по окружности.
В электродинамике отрезок, соединяющий центр окружности с точкой, используется для определения траектории и длины проводника, через который протекает электрический ток. По этому отрезку можно определить изменение магнитного поля вокруг проводника и силу, действующую на проводник со стороны магнитного поля.
Более того, этот отрезок находит свое применение и в оптике. Используя отрезок, соединяющий центр окружности с точкой, можно определить углы преломления и отражения света при прохождении через сферические поверхности, такие как, например, линзы.
Применение отрезка, соединяющего центр окружности с точкой в геометрии
1. Определение радиуса и диаметра окружности
Соединение центра окружности с любой точкой на ней позволяет определить радиус окружности. Радиус — это расстояние от центра окружности до любой ее точки. Для этого достаточно измерить длину отрезка, соединяющего центр окружности с выбранной точкой.
Кроме того, отрезок, соединяющий центр окружности с двумя любыми точками на ней, будет являться диаметром окружности. Диаметр представляет собой отрезок, проходящий через центр окружности и соединяющий две ее точки.
2. Построение перпендикуляра к хорде
Использование отрезка, соединяющего центр окружности с точкой, позволяет построить перпендикуляр к хорде окружности. Хорда — это отрезок, соединяющий две точки на окружности. Для построения перпендикуляра необходимо провести отрезок, соединяющий центр окружности с серединой хорды, и затем построить прямую, перпендикулярную данному отрезку.
3. Поиск центра окружности
Отрезок, соединяющий центр окружности с любой точкой на ней, также может использоваться для определения самого центра окружности. Для этого необходимо построить два таких отрезка, соединяющих центр окружности с различными точками, и найти их точку пересечения. Эта точка будет являться центром окружности.
Таким образом, отрезок, соединяющий центр окружности с точкой, является мощным инструментом геометрии. Его использование позволяет решать различные задачи, определять свойства окружности и строить геометрические конструкции.
Вопрос-ответ:
Что такое отрезок 3 класса в геометрии?
Отрезок 3 класса в геометрии называется отрезок, соединяющий центр окружности с любой ее точкой. Этот отрезок является радиусом окружности и имеет постоянную длину.
Какой геометрический смысл имеет отрезок 3 класса?
Отрезок 3 класса имеет геометрический смысл радиуса окружности. Он является прямой линией, соединяющей центр окружности с любой ее точкой. Длина этого отрезка является постоянной и определяет размеры окружности.
Зачем нужен отрезок 3 класса?
Отрезок 3 класса является важным элементом в геометрии и используется для решения различных задач. Он позволяет определить радиус окружности и соединяет центр окружности с ее точками. Зная длину отрезка 3 класса, можно вычислить длину окружности, площадь и дугу, а также провести перпендикуляр к отрезку.
Как вычислить длину отрезка 3 класса?
Длина отрезка 3 класса, который соединяет центр окружности с любой ее точкой, можно вычислить по формуле L = 2πr, где L — длина отрезка, π — число пи, r — радиус окружности. Если известен диаметр окружности, то длину отрезка 3 класса можно найти по формуле L = πd, где L — длина отрезка, π — число пи, d — диаметр окружности.