
Многогранники – это фигуры, имеющие тримерную структуру и состоящие из граней, ребер и вершин. Они обладают свойствами, присущими только им, и изучение их является важной задачей математики и геометрии. Многогранники бывают разных типов, и одна из интересных групп – это полуправильные многогранники.
Полуправильные многогранники – это такие многогранники, у которых все грани являются правильными многоугольниками, и вокруг каждой вершины сходится одинаковое число граней. Они отличаются своими особенностями от правильных и правильных выпуклых многогранников. Каждый полуправильный многогранник имеет свое уникальное название, основанное на его форме и свойствах.
Например, одним из самых известных полуправильных многогранников является октаэдр – фигура, состоящая из восьми равносторонних треугольников. Другим примером является икосаэдр, состоящий из двенадцати равносторонних треугольников и двадцати вершин. Еще одним полуправильным многогранником является додекаэдр, который имеет двенадцать правильных пятиугольников и двенадцать вершин.
Что такое полуправильные многогранники?

Полуправильные многогранники являются весьма интересными объектами изучения как в математике, так и в графике. Они обладают своими уникальными характеристиками и особенностями, которые делают их привлекательными для исследования. Всего в существует 13 видов полуправильных многогранников, каждый из которых имеет свое название и характеристики.
Полуправильные многогранники имеют разнообразные формы, начиная от додекаэдра и икосаэдра до тетраэктодекаэдра и стрелка. Благодаря своей уникальной геометрии и симметрии, полуправильные многогранники можно найти в различных областях науки и искусства.
Определение и особенности
Особенность полуправильных многогранников заключается в том, что они имеют лицевые грани, которые являются правильными многоугольниками, а также ребра и вершины, у которых количество и расположение отличается от тех, что представлены в полностью правильных многогранниках.
Полуправильные многогранники относятся к классу выпуклых многогранников, то есть к тем, у которых все грани, рёбра и вершины лежат на одной стороне плоскости. Они также отличаются от правильных многогранников тем, что могут иметь различное число граней.
Классификация полуправильных многогранников
Существует несколько способов классифицировать полуправильные многогранники. Одним из них является разделение на две категории: Архимедовы многогранники и Каталановы многогранники.
| Категория | Описание |
|---|---|
| Архимедовы многогранники | Это полуправильные многогранники, у которых все грани являются правильными многоугольниками и количество граней одного типа может быть различным. |
| Каталановы многогранники | Это полуправильные многогранники, у которых грани неправильной формы и их число и типы граней строго определены. |
Примеры полуправильных многогранников
Некоторые известные примеры полуправильных многогранников включают в себя додекаэдр, икосаэдр, октаэдр и кубоктаэдр. Каждый из них обладает своими уникальными свойствами и характеристиками.
Другие названия полуправильных многогранников
Полуправильные многогранники: примеры и характеристики
Примеры полуправильных многогранников:
- Тетраэдр – один из наиболее известных полуправильных многогранников. Он имеет 4 треугольных грани и 4 вершины, у каждой из которых встречается 3 грани.
- Гексаэдр (куб) – знакомая форма, у которой 6 квадратных граней и 8 вершин, каждая из которых имеет 3 грани.
- Октаэдр – многогранник с 8 треугольными гранями и 6 вершинами, где каждая вершина окружена 4 гранями.
- Додекаэдр – полуправильный многогранник, состоящий из 12 правильных пятиугольных граней и 20 вершин. У каждой вершины ровно 3 грани.
- Икосаэдр – многогранник с 20 правильными треугольными гранями и 12 вершинами, у каждой из которых 5 граней.
Характеристики полуправильных многогранников:
Полуправильные многогранники можно описать с помощью таких характеристик:
- Количество граней;
- Количество вершин;
- Количество ребер;
- Типы граней и их количество;
- Симметрия структуры многогранника;
- Максимальное и минимальное число граней, сходящихся в одной вершине.
Изучение полуправильных многогранников имеет важное значение в геометрии и математике в целом. Они применяются в различных областях, включая архитектуру, химию и кристаллографию, и представляют собой уникальные объекты с интересными свойствами.
Свойства и классификация полуправильных многогранников
Свойства полуправильных многогранников
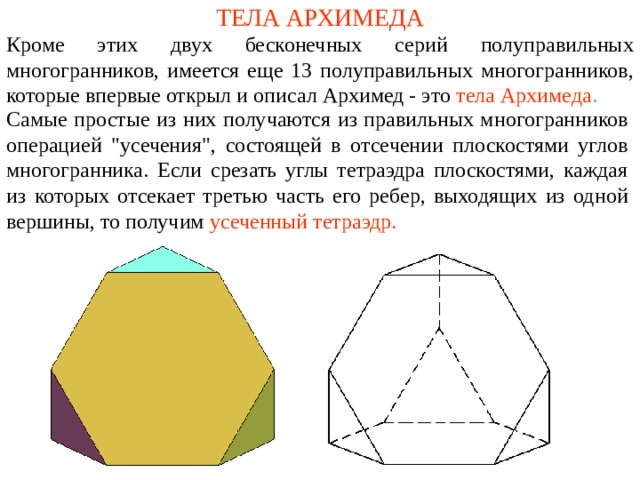
1. Все грани полуправильных многогранников являются правильными многоугольниками. Это значит, что все стороны каждой грани равны между собой, а углы между сторонами равны. Благодаря этому свойству полуправильные многогранники выглядят симметричными и эстетичными.
2. Вокруг каждой вершины полуправильного многогранника сходится одинаковое количество граней. Это означает, что все полуправильные многогранники являются выпуклыми.
3. Каждая грань полуправильного многогранника может иметь только один тип многоугольника. То есть, если одна грань является треугольником, то все остальные грани также будут треугольниками. Благодаря этому свойству полуправильные многогранники могут быть легко классифицированы.
Классификация полуправильных многогранников
Существует всего 13 различных полуправильных многогранников. Они могут быть классифицированы на основе типов и числа граней. Вот некоторые из наиболее известных полуправильных многогранников:
| Имя | Тип граней | Число граней |
|---|---|---|
| Тетраэдр | Треугольники | 4 |
| Гексаэдр (куб) | Квадраты | 6 |
| Октаэдр | Равносторонние треугольники | 8 |
| Додекаэдр | Правильные пятиугольники | 12 |
| Икосаэдр | Равносторонние треугольники | 20 |
Это лишь некоторые из примеров полуправильных многогранников. Каждый из этих многогранников имеет свои уникальные свойства и характеристики, которые делают их интересными для изучения.
История изучения полуправильных многогранников
Первые упоминания о полуправильных многогранниках были найдены в письмах Архимеда, где он описывал свои открытия в области геометрии. Он назвал некоторые из них «неподходящими многогранниками», так как при их конструировании он использовал особые комбинации граней.
В средние века эта область геометрии была неизвестной и забытой, однако в 19 веке интерес к полуправильным многогранникам возродился. Благодаря работы Леонарда Эйлера и Луи Платона, стало возможным систематизировать и изучить полуправильные многогранники.
Великий немецкий математик Карл Фридрих Гаусс внес большой вклад в изучение полуправильных многогранников. Он разработал теорию, которая объединила разные типы полуправильных многогранников в одну классификацию. Эта теория стала основой для дальнейших исследований и привлекла множество ученых со всего мира.
В настоящее время исследование полуправильных многогранников активно продолжается. С помощью компьютерных моделей и новых методов анализа, ученые находят новые типы и свойства этих геометрических фигур, что в свою очередь расширяет наше понимание о мире геометрии.
Полуправильные многогранники в природе и искусстве
В природе можно найти много примеров полуправильных многогранников. Например, оболочка воробьиных яиц имеет форму икосаэдра, одного из полуправильных многогранников. Кристаллы также могут образовываться в форме полуправильных многогранников. Эти формы имеют определенные геометрические свойства, что делает их особенно привлекательными для исследования и изучения.
Полуправильные многогранники в искусстве
Помимо присутствия в природе, полуправильные многогранники также находят свое применение в искусстве. В архитектуре и дизайне их уникальные геометрические формы используются для создания интересных и привлекательных сооружений и объектов. Многие художники и скульпторы также используют полуправильные многогранники в своих работах, чтобы создать впечатляющие и гармоничные композиции.
Исследование полуправильных многогранников
Полуправильные многогранники являются предметом интереса для математиков и ученых, которые исследуют их свойства и структуру. Изучение полуправильных многогранников помогает нам понять и описать геометрические формы в природе и искусстве. Это позволяет нам расширить наши знания о мире вокруг нас и создать новые впечатляющие и функциональные объекты и сооружения.
Применение полуправильных многогранников в науке и технологиях
Полуправильные многогранники, также известные как архимедовы тела, представляют собой геометрические фигуры, состоящие из равных многоугольных граней и равных чисел граней, сходящихся в каждой вершине.
Наука
В научных исследованиях полуправильные многогранники находят применение в различных областях. Например, они используются в химии для описания структуры молекул. Благодаря своей геометрии, полуправильные многогранники помогают ученым предсказывать свойства и поведение различных химических соединений.
Также полуправильные многогранники широко применяются в математике. Они являются основой для изучения симметрии и групп симметрии. Кроме того, полуправильные многогранники используются в топологии, теории графов, и других разделах математики.
Технологии
В технологиях полуправильные многогранники находят применение в дизайне упаковки и создании архитектурных конструкций. Благодаря своей уникальной форме, полуправильные многогранники могут быть использованы для создания красивых и прочных структур, имеющих особенности, такие как минимальная площадь поверхности или максимальная пространственная эффективность.
| Применение | Область |
|---|---|
| Моделирование молекул | Химия |
| Изучение симметрии | Математика |
| Дизайн упаковки | Технологии |
| Архитектурные конструкции | Технологии |
Вопрос-ответ:
Что такое полуправильные многогранники?
Полуправильные многогранники — это многогранники, у которых все грани являются правильными многоугольниками, но все вершины не являются одинаковыми.
Какие многоугольники могут быть гранями полуправильных многогранников?
Гранями полуправильных многогранников могут быть треугольники, квадраты, пятиугольники и т.д., но все грани должны быть одинаковыми многоугольниками.
Какие особенности у полуправильных многогранников?
Полуправильные многогранники имеют ряд особенностей. Во-первых, у них есть ось симметрии, а во-вторых, они не могут быть вписаны в сферу.
Какие полуправильные многогранники наиболее известны?
Наиболее известными полуправильными многогранниками являются октаэдр, икосаэдр и додекаэдр. Они имеют красивую и симметричную структуру и широко используются в различных областях, включая химию и геометрию.
Какие свойства полуправильных многогранников можно изучать?
Полуправильные многогранники обладают множеством интересных свойств, которые можно изучать. Например, основные свойства, такие как число граней, число вершин и число ребер, могут быть рассмотрены. Также можно изучать их симметрию, объем и поверхностную площадь. Это позволяет разрабатывать математические модели и применять полуправильные многогранники в различных практических задачах.