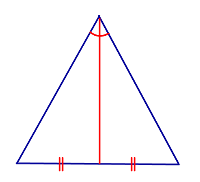
Равнобедренный треугольник — это треугольник, у которого две стороны и два угла равны друг другу. В таком треугольнике есть три различные стороны: основание и две боковые стороны. Основание — это наибольшая сторона, которая лежит между двумя вершинами равных углов. Боковые стороны расположены по обеим сторонам основания и имеют одинаковую длину.
Названия сторон равнобедренного треугольника могут быть различны, их выбор зависит от контекста. Однако существуют общепринятые обозначения. Основание треугольника обычно обозначается буквой ‘b’ или ‘a’, а боковые стороны — буквами ‘c’ и ‘d’. Вершины треугольника можно обозначать буквами или использовать буквенные индексы (‘A’, ‘B’, ‘C’ и т.д.).
Сторона треугольника — это отрезок, соединяющий две вершины. В равнобедренном треугольнике таких сторон всего три: основание и две боковые стороны. Основание является наибольшей стороной треугольника и обозначается как ‘b’. Боковые стороны, как уже было сказано, имеют одинаковую длину и обозначаются как ‘c’ и ‘d’.
Основные элементы равнобедренного треугольника
Основанием равнобедренного треугольника называется одна из его сторон, которая отличается от двух других. Обычно она обозначается буквой «a».
Боковые стороны равнобедренного треугольника — две равные между собой стороны, которые обычно обозначают буквами «b» и «c». Они соединяют вершины треугольника с основанием.
Вершины равнобедренного треугольника — точки пересечения сторон треугольника. Обычно обозначаются буквами «A», «B» и «C».
Равнобедренный треугольник обладает некоторыми специфическими свойствами, такими как равенство углов при основании, равенство высот, равенство биссектрис и т.д. Понимание основных элементов равнобедренного треугольника позволяет проще анализировать его свойства и решать задачи, связанные с данным типом треугольника.
Основание равнобедренного треугольника
Основание равнобедренного треугольника играет важную роль в его геометрических свойствах. Например, длина основания определяет высоту треугольника, которая в свою очередь влияет на его площадь. Кроме того, основание дает треугольнику устойчивость и определяет его форму.
В равнобедренном треугольнике основание равностороннего треугольника является одной из его равных сторон. Таким образом, равнобедренный треугольник имеет две равные боковых стороны и две равные угловые вершины, а основание служит связующим элементом между ними.
Важно отметить, что основание равнобедренного треугольника не является его самым коротким или самым длинным отрезком. Оно просто определяет границы треугольника и его форму, в то время как боковые стороны создают равность его углов.
Что такое основание равнобедренного треугольника
В равнобедренном треугольнике основание является горизонтальной стороной, на которой лежат две вершины треугольника. Это самая нижняя сторона треугольника, которая отделяет вершины от остальных сторон.
Основание равнобедренного треугольника обладает несколькими важными свойствами. Во-первых, длина основания равна сумме длин боковых сторон, умноженной на коэффициент подобия. Во-вторых, основание является основной опорной линией треугольника и определяет его устойчивость и форму. И, наконец, основание играет ключевую роль в вычислении площади равнобедренного треугольника по формуле 1/2 x основание x высота.
| Основание | Свойства |
|---|---|
| Горизонтальная сторона | Равна сумме длин боковых сторон |
| Опорная линия | Обеспечивает устойчивость треугольника |
| Основа для вычисления площади | Используется в формуле площади треугольника |
Важно отметить, что основание равнобедренного треугольника может быть выбрано любой из его сторон, если только треугольник является равнобедренным. Это облегчает решение геометрических задач, включающих равнобедренные треугольники, и позволяет использовать различные подходы и стратегии в их решении.
Свойства основания равнобедренного треугольника
- Основание равнобедренного треугольника является самой длинной из его сторон.
- Основание делит треугольник на две равные части, которые называются равными ногами треугольника.
- Линия, проведенная из вершины треугольника к середине основания, называется высотой треугольника. Высота равнобедренного треугольника делит его на два прямоугольных треугольника, которые являются подобными друг другу.
- Угол между основанием и одним из его равных боковых сторон является прямым углом.
Свойства основания равнобедренного треугольника являются важными при решении задач геометрии и могут помочь в определении других характеристик этого треугольника, таких как площадь или углы.
Примеры основания равнобедренного треугольника
Ниже приведены примеры основания равнобедренного треугольника:
- Основание треугольника ABC равно стороне AB, а боковые стороны — сторонам AC и BC.
- Основание треугольника XYZ равно стороне XY, а боковые стороны — сторонам XZ и YZ.
- Основание треугольника PQR равно стороне PQ, а боковые стороны — сторонам PR и QR.
Все эти треугольники являются равнобедренными, так как у них две стороны равны между собой, а третья сторона — основание, отличается от них.
Боковые стороны равнобедренного треугольника
Так как равнобедренный треугольник обладает симметрией, боковые стороны равны друг другу и образуют равные углы с основанием. Именно благодаря этим равным сторонам и углам, треугольник получает свое название «равнобедренный».
Если обозначить длину боковых сторон треугольника как a, а длину стороны основания как b, то можно записать следующие равенства:
- a = b
- ∠A = ∠C
Где ∠A и ∠C — это вершины треугольника, которые соединяются с основанием.
Важно отметить, что равные боковые стороны определены только для равнобедренных треугольников. В противном случае, треугольник будет называться разносторонним треугольником, где все стороны имеют разные длины.
Какие бывают боковые стороны равнобедренного треугольника
Боковые стороны равнобедренного треугольника называются равными сторонами или равными катетами. Они всегда располагаются с обеих сторон от основания треугольника и соединяют основание с вершинами.
Все боковые стороны равнобедренного треугольника имеют одинаковую длину и обозначаются буквой «b». Основание треугольника обозначается буквой «a». Буквой «c» обозначается гипотенуза равнобедренного треугольника, которая является высотой от вершины до основания.
| Сторона | Длина | Обозначение |
|---|---|---|
| Боковая сторона | b | AB, AC |
| Основание | a | BC |
| Гипотенуза | c | AB = AC = c |
Зная длину одной из боковых сторон и длину основания, можно легко вычислить высоту треугольника и его площадь с помощью формулы S=1/2*a*h, где S — площадь треугольника, a — длина основания, h — высота треугольника.
Таким образом, боковые стороны равнобедренного треугольника являются равными катетами и имеют одинаковую длину. Они соединяют основание с вершинами треугольника и являются ключевыми элементами данной геометрической фигуры.
Свойства боковых сторон равнобедренного треугольника
Равнобедренный треугольник отличается от других треугольников тем, что имеет две равные стороны. В таком треугольнике существуют определенные свойства боковых сторон, которые помогают в вычислениях и решении геометрических задач.
Основное свойство боковых сторон равнобедренного треугольника заключается в том, что они равны друг другу. То есть, если две стороны треугольника равны, то они являются боковыми сторонами. Это свойство позволяет выполнять определенные вычисления и преобразования в равнобедренных треугольниках.
В равнобедренном треугольнике также существуют углы, которые определяются боковыми сторонами. Эти углы называются прилежащими углами. Они равны между собой и обозначаются как α и β. Прилежащие углы являются острыми углами и находятся напротив боковых сторон.
Иногда для вычисления или доказательства утверждений в равнобедренных треугольниках нужно знать длину боковых сторон. Для этого можно использовать различные формулы и теоремы в зависимости от известных данных и требуемых результатов.
| Формула/теорема | Описание |
|---|---|
| Теорема косинусов | Позволяет вычислить длину боковой стороны, если известны длины других сторон и прилежащий угол. |
| Формула высоты | Позволяет найти длину боковой стороны, если известны длина основания и высоты, опущенной на это основание. |
Зная свойства боковых сторон равнобедренного треугольника, можно легче решать геометрические задачи, находить отношения между длинами сторон и углами, а также проводить различные вычисления, в том числе находить значение других сторон и углов треугольника.
Вопрос-ответ:
Как называется сторона равнобедренного треугольника, которая отличается от двух других?
Эта сторона называется основанием равнобедренного треугольника. Она отличается от двух боковых сторон, которые имеют одинаковую длину.
Что такое боковые стороны равнобедренного треугольника?
Боковые стороны равнобедренного треугольника — это две стороны, которые имеют одинаковую длину и отличаются от основания треугольника.
Как называются точки пересечения боковых сторон равнобедренного треугольника с основанием?
Точки пересечения боковых сторон равнобедренного треугольника с основанием называются вершинами треугольника. Такой треугольник имеет две вершины.
Может ли основание равнобедренного треугольника быть вертикальной стороной?
Да, основание равнобедренного треугольника может быть вертикальной стороной. Оно может быть любым из трех сторон треугольника, включая вертикальную сторону.
Возможно ли, чтобы все стороны равнобедренного треугольника были одинаковой длины?
Нет, в равнобедренном треугольнике две стороны всегда будут одинаковыми, а третья сторона, которая является основанием, будет отличаться.