Вектор — это основное понятие в физике и математике, которое используется для описания физических и математических величин, имеющих и направление, и величину. Он играет важную роль в многих областях науки и техники, таких как механика, геометрия и электромагнетизм. Понимание векторов и их применение является одним из ключевых элементов в изучении физики и математики.
Основные характеристики и свойства вектора
Каждый вектор характеризуется двумя основными свойствами: направлением и величиной. Направление вектора показывает, куда он направлен в пространстве. Величина вектора представляет собой численное значение, выражающее его длину или магнитуду. Для обозначения вектора используется стрелка или буква с надстрочной стрелкой, указывающей на направление вектора.
Применение векторов в физике и математике
Векторы широко используются в физике и математике для описания физических явлений и решения различных задач. В механике векторы используются для описания движения тела, силы и импульса. В геометрии векторы используются для описания пространственных отношений и геометрических фигур. В электромагнетизме векторы используются для описания электрического поля, магнитного поля и электромагнитной индукции.
Изучение векторов в физике и математике помогает развить навыки анализа и решения проблем, а также предоставляет инструменты для понимания и объяснения физических и математических явлений. Понимание векторов и их применение играет важную роль в развитии науки и техники, а также применяется в множестве сфер нашей повседневной жизни.
Что называется вектором: основные понятия и применение
Основные понятия, связанные с векторами, включают:
Направление: описывает, в каком направлении указывает вектор. Обычно используются углы или направления относительно осей координат.
Величина: показывает длину или размер вектора. Величина может быть положительной или нулевой, но не может быть отрицательной.
Начальная точка: определяет местоположение, с которого начинается вектор. Начальная точка является отправной точкой для определения конечной точки вектора.
Векторы используются в физике и математике для моделирования и анализа физических явлений. Они могут представлять силу, скорость, ускорение, смещение и другие физические величины. Векторы позволяют рассчитывать суммарные силы, вычислять скорость и определять направление движения тела.
Векторы также широко используются в геометрии и анализе данных. Они помогают определять взаимное расположение объектов, находить решения систем уравнений и моделировать пространственные объекты.
Важно отметить, что векторы являются абстрактными математическими объектами и могут быть представлены числовыми значениями или символами. Они позволяют упростить сложные физические и математические задачи и обеспечивают удобный способ описания и анализа различных явлений.
Понятие вектора
В физике векторы используются для описания физических величин, таких как сила, скорость, ускорение и т. д. Например, вектор силы указывает на направление силы и ее величину. Вектор скорости указывает на направление движения и его скорость.
В математике векторы используются для решения геометрических задач. Они могут быть представлены в виде точек, направленных от одной точки к другой, или в виде столбцов или строк чисел. Векторы могут использоваться для определения длины, угла и других свойств фигур.
Векторы могут быть складываться и вычитаться, умножаться на число и использоваться для описания преобразований в пространстве. Они широко используются в физике, математике, компьютерной графике и других областях.
Таким образом, понятие вектора является фундаментальным в физике и математике. Оно позволяет описывать и решать различные задачи, связанные с величинами и направлениями в пространстве.
| Применение в физике: | Применение в математике: |
|---|---|
| Описание силы, ускорения, скорости и других физических величин. | Решение геометрических задач, определение длины, угла и других свойств фигур. |
| Описание движения тела, преобразования координат и других физических процессов. | Решение систем уравнений, определение скалярного и векторного произведения и других математических операций. |
Определение вектора
Модуль вектора — это его длина, которая определена как положительное число и обозначена символом |а| (где а — вектор).
Направление вектора может быть задано числовым значением — углом между вектором и определенным направлением на плоскости. Например, угол между вектором и осью Ox.
Также вектор может быть задан в виде упорядоченной пары чисел (x, y) — компонент вектора.
Определение вектора может быть представлено таблицей:
| Величина | Обозначение |
|---|---|
| Модуль вектора | |а| |
| Направление вектора | θ |
| Компоненты вектора | (x, y) |
Векторы могут быть сложены или умножены на число, и обладают некоторыми свойствами, такими как коммутативность и ассоциативность.
Векторы широко применяются в физике и математике для описания многих физических явлений и процессов, таких как движение тел, силы, электромагнетизм и т.д.
Операции с векторами
Существует несколько основных операций с векторами:
- Сложение векторов: для сложения двух векторов их концы выстраиваются так, чтобы начало второго вектора совпадало с концом первого вектора. Результирующий вектор — это вектор, направление которого от начала первого вектора до конца второго вектора.
- Вычитание векторов: для вычитания векторов требуется их сложение с вектором, обратным вычитаемому вектору. Или, другими словами, векторы с одинаковыми началами, но с противоположными направлениями складываются вместе.
- Умножение вектора на скаляр: при умножении вектора на скаляр, каждая составляющая вектора умножается на этот скаляр. Это влияет на величину вектора и может изменить его направление, если скаляр отрицательный.
- Деление вектора на скаляр: при делении вектора на скаляр, каждая составляющая вектора делится на этот скаляр. Результатом является вектор той же направленности, но с измененной величиной.
Эти операции с векторами имеют ряд математических свойств и удовлетворяют определенным правилам, которые обеспечивают их корректное применение в физике и математике.
Векторы являются важными инструментами для анализа и решения различных задач, поэтому понимание операций с векторами — это фундаментальный навык для студентов и профессионалов в области физики и математики.
Векторы в физике
Вектор – это физическая величина, которая характеризуется не только числовым значением, но и направлением. Вектор можно представить в виде направленного отрезка, начало которого определяет точка приложения вектора, а конец – его направление. Длина отрезка соответствует величине вектора.
Векторы в физике используются для описания различных физических величин, таких как сила, скорость, ускорение и др. С помощью векторов можно определить, например, силу, с которой тело действует на другое тело, или направление и скорость движения объекта.
Роль векторов в описании движения
Векторы играют важную роль в описании движения в физике и математике. Они позволяют точно определить направление и величину движения объекта.
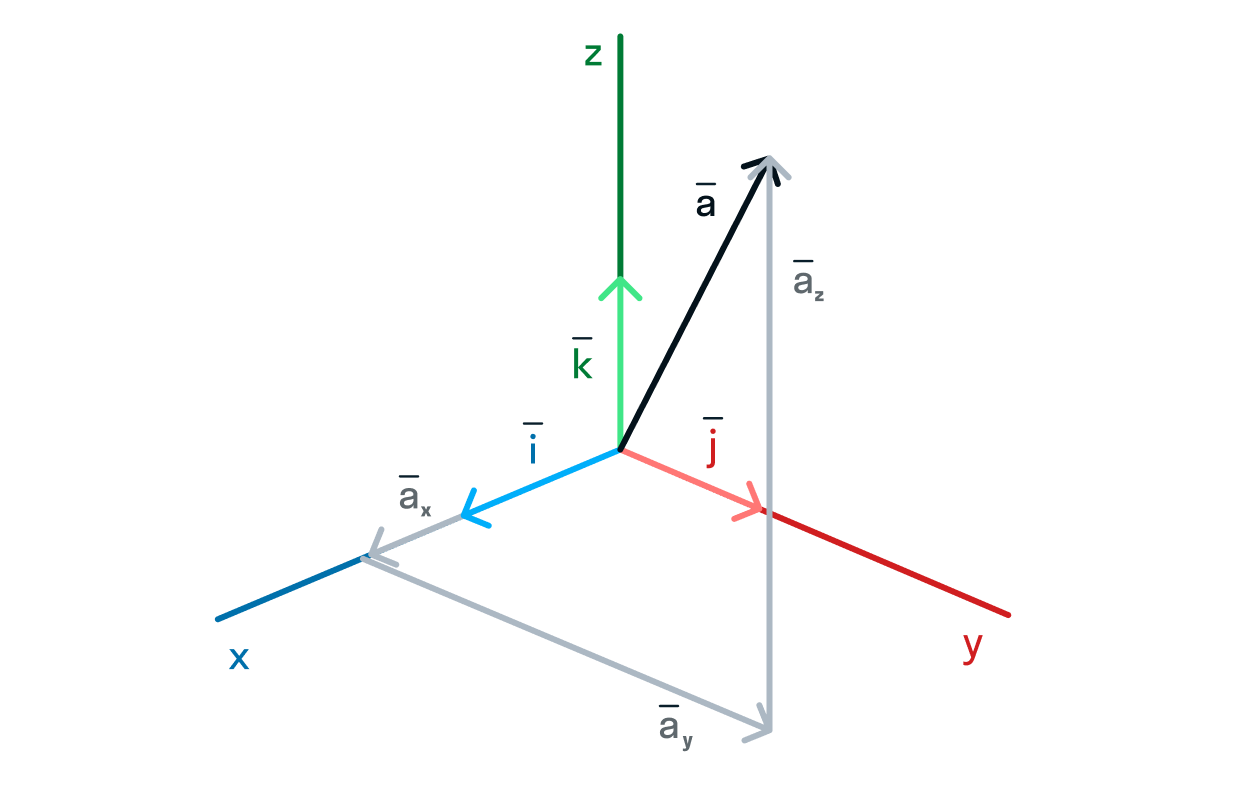
Для описания движения в трехмерном пространстве используются трехмерные векторы, которые имеют три компоненты: x, y и z. Компоненты вектора представляют собой числа, которые указывают на изменение координаты объекта в каждом измерении.
Один из основных примеров применения векторов в описании движения — это вектор скорости. Вектор скорости показывает изменение положения объекта со временем и имеет направление и величину.
| Понятие | Описание |
|---|---|
| Скорость | Вектор, определяющий изменение положения объекта за единицу времени. |
| Ускорение | Вектор, показывающий изменение скорости объекта за единицу времени. |
| ДисплACEMENT | Вектор, который соединяет начальное и конечное положение объекта. |
| Сила | Вектор, описывающий воздействие на объект и вызывающий его движение. |
Благодаря векторам мы можем более точно описывать движение объектов в пространстве. Векторы позволяют нам рассчитывать скорость, ускорение и другие характеристики движения, что является важным элементом в физике и математике.
Концепция силовых векторов
В физике, силы играют важную роль в изучении движения тела и взаимодействия между объектами. Концепция силовых векторов позволяет нам точно определить силу и ее направление, используя математическую формулировку векторов.
Сила представляется в виде вектора, который имеет определенный модуль (величину) и направление. Векторы используются для описания всех характеристик силы, включая ее величину (измеряемую в ньютонах) и направление, в котором она действует.
Например, если мы рассматриваем силу, действующую на объект в двухмерном пространстве, мы можем представить ее с помощью вектора, имеющего две компоненты: горизонтальную и вертикальную. Модуль этого вектора будет определять величину силы, а его направление — направление силы.
Силовые векторы также могут быть сложены и вычитаны, чтобы определить результирующую силу, действующую на объект. Это делается путем сложения или вычитания каждой компоненты вектора по отдельности.
Концепция силовых векторов является важным инструментом для решения физических задач. Используя математическую формулировку векторов, мы можем более точно определить и анализировать силы, действующие на объекты в физической системе.
| Примеры применения: |
|---|
| Определение результирующей силы, действующей на тело |
| Анализ баланса сил в статическом равновесии |
| Расчет скорости и ускорения тела под действием силы |
| Определение равновесия системы сил |
Векторы являются неотъемлемой частью физики и математики. Концепция силовых векторов предоставляет нам мощный инструмент для описания и анализа сил и их воздействия на объекты в физической системе.
Векторы в математике
В математике векторы представляют собой объекты, которые имеют как направление, так и величину.
Они могут быть представлены в виде стрелок на плоскости или в пространстве и обозначаются с помощью буквы или полужирным шрифтом.
Векторы могут быть описаны с помощью координат или своих компонентов.
Координаты вектора – это числа, которые показывают его положение в пространстве.
Компоненты вектора – это проекции вектора на координатные оси.
Векторы могут быть сложены или умножены на число.
Сложение векторов происходит по правилу треугольника или по правилу параллелограмма.
Умножение вектора на число приводит к его растяжению или сжатию.
Векторы широко используются в физике для описания движения тел, сил и многих других явлений.
Они позволяют точно описывать и предсказывать результаты физических экспериментов и являются основным инструментом решения многих физических задач.
Также векторы активно применяются в математическом анализе, где они являются одним из ключевых понятий.
Векторные пространства, дифференциальные операторы и теория функций, основанные на понятии вектора, являются фундаментальными для математического анализа и его приложений.
Вопрос-ответ:
Что такое вектор в физике и математике?
Вектор — это математический объект, который характеризуется направлением и величиной. В физике вектор используется для описания таких величин, как скорость, сила, сила тяжести и т.д. В математике вектор используется для решения задач геометрии и алгебры, а также векторные операции, такие как сложение, вычитание и умножение на число.
Какие основные понятия связаны с векторами в физике и математике?
Основными понятиями, связанными с векторами, являются направление, величина, и операции сложения и умножения на число. Направление определяется углом относительно определенной оси или вектора. Величина является числовой характеристикой вектора и может быть представлена величиной физической величины, такой как метры в физике и числами в математике. Операции сложения и умножения на число позволяют выполнять различные вычисления с векторами.
Какие применения векторов существуют в физике?
Векторы имеют широкое применение в физике. Они используются для описания движения тела (скорости, ускорения), сил, вращения, электромагнитных полей и других физических явлений. Векторные операции, такие как сложение и умножение на число, позволяют анализировать и решать физические задачи с высокой точностью и эффективностью.
Как векторы применяются в математике?
Векторы используются в математике для решения геометрических и алгебраических задач. Они используются для вычисления расстояний и углов между точками и прямыми, для решения систем уравнений и линейных преобразований. Векторы также применяются в анализе данных, машинном обучении и других областях математики, где необходимо представление и манипуляция многомерными данными и величинами.
Что такое вектор в физике?
Вектор в физике — это математический объект, который характеризует физическую величину и обладает направлением и величиной. Направление вектора задается линией, а его величина — длиной этой линии. Вектор используется для описания многих физических величин, таких как сила, скорость, ускорение.