
Линейная функция является одной из наиболее простых и понятных математических моделей, позволяющих описывать зависимость одной величины от другой. Она представляет собой прямую линию на графике, где каждому значению независимой переменной (в данном случае времени) соответствует определенное значение зависимой переменной (координаты).
Основной характеристикой линейной функции является постоянный прирост или убывание зависимой переменной при изменении независимой переменной на единицу. Это означает, что график такой функции представляет собой прямую линию, наклон которой определяет скорость изменения координаты с течением времени.
Линейная функция может быть представлена в виде уравнения y = kx + b, где y — значение зависимой переменной (координата), x — значение независимой переменной (время), k — коэффициент наклона графика (скорость изменения координаты) и b — начальное значение зависимой переменной (координаты в начальный момент времени).
Линейная функция: определение и примеры
Линейная функция представляет собой функцию вида y = kx + b, где x и y — координаты точки на графике функции, k — коэффициент наклона прямой, а b — свободный член, отвечающий за сдвиг графика функции в вертикальном направлении.
Примеры линейных функций:
| Функция | График |
|---|---|
| y = 2x + 3 |  |
| y = -0.5x + 2 |  |
Графики линейных функций представляют собой прямые линии на плоскости. Коэффициент наклона k определяет угол прямой относительно оси x, а свободный член b указывает на пересечение прямой с осью y.
Линейная функция является простейшим примером функции и используется для моделирования многих взаимосвязей в различных областях науки и техники. Она имеет множество приложений в физике, экономике, информатике и других научных дисциплинах.
Что такое линейная функция?
Линейная функция имеет вид y = kx + b, где x — независимая переменная (обычно представляющая время или расстояние), y — зависимая переменная (обычно представляющая значение, которое зависит от x), k — коэффициент, определяющий угол наклона прямой, и b — свободный член, определяющий смещение прямой по оси y.
У линейной функции есть несколько важных свойств. Во-первых, она всегда представляет прямую линию. Во-вторых, угол наклона этой линии определяется коэффициентом k. Если k положительный, то прямая наклонена вверх справа налево, если k отрицательный, то вниз справа налево. Если k равен нулю, то прямая горизонтальна. В-третьих, свободный член b определяет точку пересечения прямой с осью y.
Пример 1:
Рассмотрим функцию y = 2x + 1. График этой функции представляет собой прямую линию, которая наклонена вверх справа налево и пересекает ось y в точке (0,1). Коэффициент k равен 2, что означает, что каждый раз, когда x увеличивается на 1, значение y увеличивается на 2.
Пример 2:
Рассмотрим функцию y = -0.5x + 3. График этой функции представляет собой прямую линию, которая наклонена вниз справа налево и пересекает ось y в точке (0,3). Коэффициент k равен -0.5, что означает, что каждый раз, когда x увеличивается на 1, значение y уменьшается на 0.5.
Линейные функции широко используются в различных областях науки и техники. Они позволяют анализировать зависимости между различными переменными и делать прогнозы о их взаимосвязи.
Свойства линейной функции
Свойства линейной функции включают:
1. Прямая линейная зависимость: В линейной функции изменение одной переменной приводит к соответствующему изменению другой переменной в пропорциональном соотношении. Это означает, что график линейной функции представляет собой прямую линию.
2. Угловой коэффициент: Угловой коэффициент k определяет наклон прямой линии графика линейной функции. Он показывает, насколько изменяется y при изменении x на единицу. Если k положительный, то линия наклонена вверх, а если k отрицательный, то линия наклонена вниз.
3. Свободный член: Свободный член b представляет собой значение y, когда x равно нулю. Он определяет, где линия пересекает ось y.
4. Домен и область: Доменом линейной функции является множество всех допустимых значений x, а областью — множество всех соответствующих значений y. В случае линейной функции, домен и область являются всеми действительными числами.
5. Таблица значений: Линейная функция может быть представлена в виде таблицы, показывающей соответствующие значения x и y. Это помогает визуализировать зависимость между переменными и построить график.
Изучение свойств линейной функции позволяет анализировать и понимать её поведение, что является важным инструментом в научных и технических областях.
График линейной функции
Линейная функция представляет собой функцию, график которой представляет собой прямую линию на координатной плоскости. График линейной функции имеет особенность, что каждая точка на прямой соответствует определенному значению аргумента и соответствующему значению функции.
На графике линейной функции можно выделить две важные точки: начальную точку и точку, через которую проходит прямая. Начальная точка соответствует значению функции при аргументе равном нулю. Точка, через которую проходит прямая, характеризует наклон прямой и определяется двумя значениями: аргументом и значением функции.
Если функция представлена уравнением вида y = kx + b, где k — наклон прямой, а b — значение функции при аргументе равном нулю, то коэффициент k определяет угол наклона прямой: если k > 0, то наклон прямой вверх, если k < 0, то наклон прямой вниз.
Таким образом, график линейной функции представляет собой прямую линию, проходящую через две важные точки: начальную точку и точку, через которую проходит прямая. Наклон прямой определяется коэффициентом k в уравнении функции. График линейной функции используется для изучения зависимости координаты от времени и во многих других областях науки и техники.
Формула линейной функции
Общий вид формулы линейной функции
Y = a * X + b
Где:
- Y — значение зависимой переменной
- a — коэффициент, определяющий наклон прямой
- X — значение независимой переменной
- b — свободный член, определяющий смещение прямой
Коэффициент a определяет, насколько быстро будет изменяться значение зависимой переменной (Y) при изменении значения независимой переменной (X). Свободный член b представляет начальное значение зависимой переменной (Y) при значении независимой переменной (X), равном нулю.
Пример использования формулы линейной функции
Пусть у нас есть функция, описывающая зависимость расстояния (Y) от времени (X). Если мы хотим найти расстояние через 5 секунд (X = 5), и известно, что при времени равном нулю (X = 0) расстояние было 10 метров (Y = 10), то мы можем использовать формулу линейной функции:
Y = a * X + b
10 = a * 0 + b
10 = b
Таким образом, свободный член b равен 10. Используя это значение и предположив, что коэффициент a равен 2 (для увеличения расстояния в 2 раза каждую секунду), мы можем найти расстояние через 5 секунд:
Y = 2 * 5 + 10
Y = 20
Таким образом, расстояние через 5 секунд составляет 20 метров.
Примеры линейных функций
Пример 1: Функция y = 2x + 3, где x — независимая переменная, а y — зависимая переменная. Коэффициент 2 перед переменной x определяет угловой коэффициент прямой линии, а константа 3 — смещение прямой по вертикали.
Пример 2: Функция y = -0,5x + 2, где x — независимая переменная, а y — зависимая переменная. Коэффициент -0,5 перед переменной x определяет отрицательный угловой коэффициент прямой линии, а константа 2 — смещение прямой по вертикали.
Пример 3: Функция y = x, где x — независимая переменная, а y — зависимая переменная. В этом случае угловой коэффициент равен 1, и прямая проходит через начало координат.
Линейные функции часто используются для моделирования реальных процессов, таких как движение тела, рост популяции или изменение температуры. Они также могут быть полезными в математических и физических задачах, а также в экономическом анализе.
Замечание: Линейные функции можно представить в виде уравнения вида y = mx + b, где m — угловой коэффициент, a b — смещение прямой по вертикали.
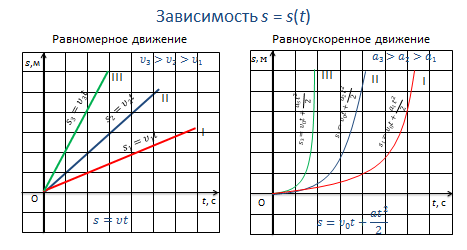
Зависимость координаты от времени
Такая зависимость может быть линейной функцией, когда координата изменяется пропорционально времени. Например, если объект движется с постоянной скоростью, то его координата будет увеличиваться или уменьшаться равномерно с каждой секундой.
В линейной зависимости координата может быть представлена уравнением вида y = kx + b, где y — координата, x — время, k — коэффициент наклона прямой, b — свободный член. Коэффициент наклона определяет скорость изменения координаты, а свободный член — начальное положение объекта в пространстве.
Знание зависимости координаты от времени позволяет предсказывать положение объекта в будущем или определять его скорость и ускорение. Это основа для решения множества задач в физике и других науках.
Как решать задачи с линейными функциями?
1. Изучите основные понятия
Перед началом решения задач с линейными функциями необходимо изучить и запомнить основные понятия. Важно знать, что линейная функция представляет собой математическое выражение вида y = kx + b, где k — наклон прямой (коэффициент наклона), b — свободный член (точка пересечения с осью ординат).
2. Определите известные и неизвестные величины
Перед решением задачи необходимо определить все известные и неизвестные величины. Известными могут быть значения переменных (x или y), значения наклона (k) или свободного члена (b). Неизвестной будет являться одна из величин.
3. Примените соответствующую формулу или метод
Для решения задач с линейными функциями применяются различные методы и формулы. Если известны значения x, k и b, можно найти значение y по формуле y = kx + b. Если известны значения y, k и b, можно найти значение x по формуле x = (y — b) / k. Если известны значения x и y, можно найти наклон прямой k по формуле k = (y — b) / x или свободный член b по формуле b = y — kx.
В некоторых случаях может потребоваться использование дополнительных методов, например, нахождение точки пересечения двух линейных функций или решение системы линейных уравнений.
4. Проверьте полученное решение
После выполнения всех расчетов рекомендуется проверить полученное решение, подставив найденные значения в исходную линейную функцию и проверив его правильность. Если значение y, полученное при подстановке, совпадает с известным значением y, то решение верно.
Понимание основных принципов решения задач с линейными функциями позволит уверенно выполнять подобные задания и успешно использовать их в практических ситуациях. Постоянная практика различных задач с линейными функциями поможет развить навык анализа и применения математических методов для работы с различными данными.
Вопрос-ответ:
Что такое линейная функция?
Линейная функция — это функция, которая задает зависимость одной переменной от другой переменной таким образом, что график этой зависимости является прямой линией.
Как можно определить, что зависимость координаты от времени является линейной функцией?
Если график зависимости координаты от времени представляет собой прямую линию, то можно сказать, что эта зависимость является линейной функцией.
Как выразить линейную функцию алгебраически?
Линейную функцию можно выразить алгебраически в виде y = mx + b, где y — значение функции, x — значение переменной, m — коэффициент наклона прямой, b — свободный член функции.
Какие примеры можно привести линейных функций?
Примерами линейных функций являются зависимости типа расстояние = скорость * время, где скорость постоянна, или температура = коэффициент * время + начальная температура.