Что такое прямоугольник и его особенности

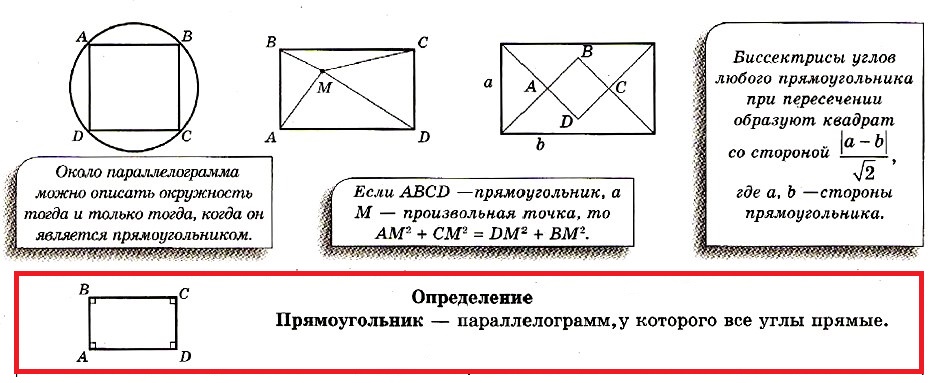
Прямоугольник – это одна из самых простых и распространенных геометрических фигур. Он обладает рядом особенностей, которые делают его удобным и полезным для различных математических и практических задач.

Основная особенность прямоугольника заключается в том, что у него есть четыре угла, каждый из которых равен 90 градусов. Это позволяет ему образовывать прямые углы с другими фигурами и поверхностями. Благодаря этому свойству прямоугольник широко применяется в архитектуре, строительстве, дизайне и других областях.

Кроме того, прямоугольник обладает параллельными сторонами, что позволяет ему быть симметричным относительно одной из своих осей. Это делает его универсальным для создания различных конструкций, ящиков, рамок, каркасов и других объектов.

Прямоугольник также обладает свойством площади, которая вычисляется как произведение его длины и ширины. Это позволяет использовать его для измерения и оценки площадей различных поверхностей, пространств и объектов.

Содержание

Определение и свойства прямоугольника

Прямоугольник имеет четыре стороны. Две противоположные стороны параллельны друг другу и равны по длине.
Углы прямоугольника равны по 90 градусов.
Диагонали прямоугольника равны по длине и делят фигуру на два равных прямоугольных треугольника.
Периметр прямоугольника равен сумме длин всех его сторон.
Площадь прямоугольника вычисляется как произведение длин его сторон.

Прямоугольник является основной фигурой при изучении геометрии и находит широкое применение в различных областях, таких как архитектура, инженерия и графика. Знание свойств прямоугольника позволяет решать задачи по расчетам площадей, периметров и других параметров этой геометрической фигуры.

Определение прямоугольника

Страницы прямоугольника называются его сторонами. Две стороны, которые находятся друг против друга и параллельны, называются основаниями прямоугольника. Другие две стороны называются боковыми сторонами.

Прямоугольник обладает несколькими важными свойствами:

Периметр прямоугольника равен сумме длин всех его сторон.
Площадь прямоугольника вычисляется как произведение длин его двух оснований.
Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины. Длина диагонали может быть вычислена с помощью теоремы Пифагора: корень суммы квадратов длин оснований.

Прямоугольники широко применяются в архитектуре, строительстве, графике и других областях, где требуется работа с плоскими фигурами. В программировании прямоугольники часто используются для задания границ и расположения элементов интерфейса.

Основные свойства прямоугольника

Форма прямоугольника является прямоугольной (прямой) – углы между его сторонами равны 90 градусов. Это делает прямоугольник особенно подходящим для строительства и дизайна.

Прямоугольник имеет две пары равных сторон, которые называются основаниями. Они параллельны друг другу и перпендикулярны к боковым сторонам.

Длина оснований называется шириной прямоугольника, а длина боковых сторон – высотой. Прямоугольник также имеет периметр (сумма всех его сторон) и площадь (произведение длины и ширины).

Основным свойством прямоугольника является равенство диагоналей – линий, соединяющих противоположные углы. Также прямоугольник является простой и понятной фигурой, которую легко использовать и изучать.

Формулы для вычисления периметра и площади прямоугольника

Периметр прямоугольника вычисляется по формуле:

P = 2 * (a + b)

где P — периметр прямоугольника, a — длина одной из его сторон, b — длина второй стороны. Для вычисления периметра необходимо сложить длины всех сторон прямоугольника и умножить полученную сумму на 2.

Площадь прямоугольника вычисляется по формуле:

S = a * b

где S — площадь прямоугольника, a — длина одной из его сторон, b — длина второй стороны. Для вычисления площади необходимо умножить длины двух сторон прямоугольника.

Зная длины сторон прямоугольника, можно легко вычислить его периметр и площадь, что позволяет более точно определить его характеристики и использовать в различных математических задачах.

Особенности прямоугольника

1. Прямоугольник имеет две пары равных углов, каждая из которых составляет 90 градусов. Такие углы называются прямыми углами. Они являются главной особенностью прямоугольника и определяют его форму.

2. Все четыре угла прямоугольника совпадают, то есть они равны между собой. Это позволяет прямоугольнику быть правильным и симметричным.

3. Диагонали прямоугольника равны между собой и делят прямоугольник на два равных треугольника. Благодаря этому, диагонали прямоугольника могут быть использованы для вычисления площади и других характеристик фигуры.

4. Прямоугольник является частным случаем параллелограмма, у которого все углы прямые. Это означает, что прямоугольник обладает всеми свойствами параллелограмма, но при этом имеет особое свойство прямых углов.

Все эти особенности прямоугольника делают его важной геометрической фигурой с широким спектром применений. Отличительные черты прямоугольника позволяют использовать его в архитектуре, строительстве, графике, математике и других областях.

Углы прямоугольника

Углы прямоугольника равны между собой. Каждый угол прямоугольника составляет 90 градусов. Это означает, что все углы в прямоугольнике одинаковы и прямые.
Углы прямоугольника дополняют друг друга. Дополнительные углы прямоугольника — это углы, которые, когда их складывают вместе, дают 180 градусов. Поскольку углы прямоугольника равны 90 градусам, дополнительный угол прямоугольника также будет равен 90 градусам.
Углы прямоугольника всегда остаются прямыми, независимо от размеров сторон. Даже если стороны прямоугольника различной длины, его углы всегда останутся прямыми. Это делает прямоугольник особо полезным для строительства и измерения, поскольку его углы могут использоваться для создания перпендикулярных линий.
Углы прямоугольника помогают определить его площадь и периметр. Площадь прямоугольника рассчитывается по формуле: S = a * b, где a и b — длины его сторон. Периметр прямоугольника равен сумме длин всех его сторон: P = 2 * (a + b).

Диагонали прямоугольника

Длины диагоналей прямоугольника связаны между собой по формуле Пифагора:

диагональ = √(длина1² + длина2²)

Диагонали прямоугольника имеют следующие свойства:

Диагонали равны по длине: AB = CD.
Диагонали делят прямоугольник на четыре равных треугольника.
Диагонали являются взаимными перпендикулярами: AB ⊥ CD.
Сумма квадратов длин диагоналей равна сумме квадратов длин сторон прямоугольника: AB² + CD² = AD² + BC² = AC² + BD².

Знание свойств и формул, связанных с диагоналями прямоугольника, позволяет удобно решать задачи, связанные с данным геометрическим объектом.

Вопрос-ответ:

Как определить прямоугольник?

Прямоугольник — это геометрическая фигура, у которой все углы равны 90 градусам, а противоположные стороны параллельны и равны между собой.

Какие особенности имеет прямоугольник?

Прямоугольник имеет несколько особенностей: все его углы прямые, противоположные стороны равны и параллельны, а диагонали равны и делят прямоугольник на два равных треугольника.

Какие формулы можно использовать для расчета свойств прямоугольника?

Для расчета площади прямоугольника можно использовать формулу: S = a * b, где a и b — длины сторон прямоугольника. Для расчета периметра прямоугольника можно использовать формулу: P = 2a + 2b, где a и b — длины сторон прямоугольника.

Как применяются прямоугольники в повседневной жизни?

Прямоугольники широко используются в повседневной жизни. Они применяются в строительстве для построения стен, окон, дверей. Также прямоугольники используются в мебельном производстве для изготовления столов, шкафов, кроватей и других предметов мебели.

Какие фигуры являются подобными прямоугольнику?

Фигуры, которые имеют прямые углы и противоположные стороны, параллельные и равные между собой, также являются подобными прямоугольнику. К ним относятся квадрат и параллелограмм.