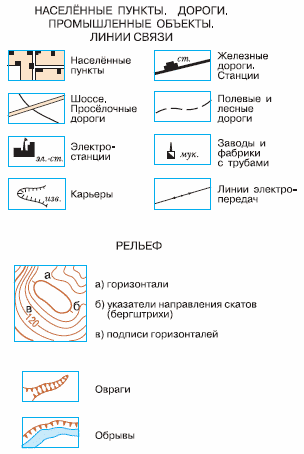
Условные обозначения — это способ представления объектов, явлений или отношений между ними с помощью символов или знаков, которые используются для обозначения определенных значений или свойств. Они представляют собой соглашения между людьми, которые позволяют передавать информацию и описывать мир вокруг нас.
Одним из примеров условных обозначений является математическая нотация. В математике используются символы, такие как «+», «-«, «*», «/», чтобы обозначить действия над числами. Они позволяют нам записывать и решать сложные математические задачи, делая их более компактными и наглядными.
В научных областях также часто применяются условные обозначения. Например, в физике для обозначения физических величин используют символы, такие как «F» для обозначения силы, «m» для обозначения массы и «a» для обозначения ускорения. Это позволяет ученым описывать и изучать различные явления и законы природы.
В программировании условные обозначения также играют важную роль. Они используются для обозначения переменных, операторов и функций. Например, в языке программирования C символ «==» используется для сравнения двух значений, а символ «=» используется для присваивания значений переменным. Такие условные обозначения помогают программистам писать читаемый и понятный код, делая его более структурированным и логическим.
Условные обозначения в представлении объектов
В представлении объектов условные обозначения играют ключевую роль, так как они позволяют создавать компактные и ясные записи о свойствах и характеристиках объектов. Они также облегчают процесс коммуникации между учеными и специалистами, позволяя использовать стандартизированные символы и сокращения.
Примеры условных обозначений в представлении объектов:
| Обозначение | Значение | Примеры применения |
|---|---|---|
| x | Координата по горизонтали или переменная | x = 5; x + 3 = 8 |
| y | Координата по вертикали или переменная | y = 3; 2y = 6 |
| a | Сторона или размер объекта | a = 10; Площадь квадрата a^2 |
| m | Масса объекта | m = 2; Энергия E = mc^2 |
Такие условные обозначения позволяют упростить запись и чтение математических и физических формул, делая их более компактными и понятными. Кроме того, они позволяют легко подставлять значения и проводить вычисления с помощью символов, не нагружая текст большим количеством слов.
Условные обозначения в представлении объектов имеют важное значение для различных научных и инженерных дисциплин, где точность и ясность выражений играют важную роль. Они помогают избегать неоднозначности и упрощают работу с объектами и их свойствами.
Роль и значение условных обозначений
Условные обозначения используются для создания формальных и точных определений объектов и позволяют нам ясно и однозначно описать их свойства и функции. Они помогают избежать двусмысленности и неоднозначности в понимании объектов и обеспечивают общепринятые стандарты в их описании.
Кроме того, условные обозначения позволяют устанавливать связи между объектами и определять их отношения. Они позволяют задавать условия для использования объектов и определять возможные варианты их взаимодействия.
Важной особенностью условных обозначений является их гибкость и универсальность. Они позволяют описывать объекты и их свойства на разных уровнях абстракции, а также присваивать объектам различные характеристики и атрибуты в зависимости от контекста и условий.
Таким образом, условные обозначения играют ключевую роль в представлении объектов и позволяют нам более точно и ясно определить их характеристики и свойства, установить связи между объектами и определить условия и ограничения их использования.
Основные виды условных обозначений
Условные обозначения представляют собой способ коммуникации и передачи информации об объектах с помощью символов, знаков или сокращений. В зависимости от области применения и целей, существуют различные виды условных обозначений. Ниже приведены основные виды условных обозначений:
- Символы и знаки — наиболее распространенный вид условных обозначений. В этом случае используются специальные символы или знаки, которые обозначают определенные понятия или объекты. Например, символы математических операций (+, -, *, /), а также знаки пунктуации (., !, ?) являются условными обозначениями, которые помогают представить определенные действия или концепции.
- Сокращения и аббревиатуры — другой популярный вид условных обозначений. С помощью сокращений и аббревиатур можно передать большое количество информации в более компактной форме. Например, сокращение «HTML» означает «HyperText Markup Language» и является условным обозначением для языка разметки веб-страниц.
- Иконки и символы — в современном мире все большую популярность набирают иконки и символы, которые помогают представить объекты и понятия без использования текста. Например, символ в виде сердца часто используется для обозначения любви или привязанности, а иконки социальных сетей (например, Facebook, Twitter, Instagram) помогают идентифицировать соответствующие платформы.
Важно знать, что условные обозначения могут иметь различную интерпретацию в разных контекстах и культурах. Поэтому при использовании условных обозначений следует учитывать аудиторию и контекст, чтобы быть уверенным, что информация будет понята и интерпретирована правильно.
Термины и определения
В мире условных обозначений существуют ряд терминов и определений, которые важно знать:
-
Условное обозначение — способ представления объектов или понятий с помощью символов или знаков, которые иначе не связаны с данными объектами. Условные обозначения позволяют нам абстрагироваться от конкретных предметов и работать с абстрактными концепциями.
-
Символ — знак, который используется для обозначения объекта или понятия. Символ может представлять собой букву, цифру, специальный знак или комбинацию символов.
-
Переменная — символ или буквенное выражение, которое представляет неизвестное значение в математических и логических выражениях. Переменные позволяют нам работать с обобщенными значениями и проводить различные операции над ними.
-
Значение — конкретное или абстрактное значение, которое может принимать символ или переменная. Значение может быть числом, строкой или иным типом данных, в зависимости от контекста использования условного обозначения.
-
Выражение — комбинация символов, переменных и операторов, представляющая математическое или логическое высказывание. Выражение может быть простым (состоящим из одного символа или переменной) или сложным (состоящим из нескольких символов, переменных и операторов).
-
Оператор — символ или знак, который используется для выполнения определенных операций над символами, переменными или выражениями. Операторы могут быть математическими, логическими или другими типами, которые определяют, как будет изменяться или взаимодействовать символы, переменные и выражения.
-
Функция — именованный блок кода, который принимает определенные аргументы и возвращает результат. Функции могут быть использованы для выполнения определенных операций над символами, переменными или выражениями и могут быть заранее определены или созданы пользователем.
Эти термины и определения являются основой для понимания условных обозначений и их использования в представлении объектов и понятий. Понимание этих терминов поможет вам легче освоить и применять концепции условных обозначений в своей работе.
Символы и графические обозначения
Символы могут представляться в виде букв, цифр или специальных знаков. Они имеют свои смысловые значения и используются для обозначения определенных объектов, явлений или процессов. Например, символ «Х» может обозначать крест, символ «О» — окружность, а символ «!» — восклицательный знак.
Графические обозначения, в свою очередь, используют изображения для представления объектов. Наиболее распространенным примером графического обозначения является пиктограмма. Пиктограммы представляют собой графические изображения, которые легко узнаваемы и наглядно передают определенный смысл. Они широко используются в дорожной, информационной и организационной сферах.
Графические обозначения также могут быть представлены в виде диаграмм, схем, графов и других визуальных элементов. Они помогают упростить восприятие информации и улучшить ее понимание.
| Символ/Изображение | Обозначение |
|---|---|
| + | Плюс (сложение) |
| — | Минус (вычитание) |
| * | Умножение |
| / | Деление |
Логические и математические символы
В условных обозначениях, также известных как предикатная логика, используются логические и математические символы для описания отношений и операций между объектами.
Логические символы используются для обозначения отношений и операций логики, таких как «и», «или», «не», «если-то». Например:
- Символ «и» (⋀) используется для обозначения конъюнкции, то есть истинности выражения, если оба его компонента истинны.
- Символ «или» (⋁) используется для обозначения дизъюнкции, то есть истинности выражения, если хотя бы один из его компонентов истинен.
- Символ «не» (¬) используется для обозначения отрицания, то есть инверсии истинности выражения.
- Символ «если-то» (→) используется для обозначения импликации, то есть истинности выражения в случае, когда первое выражение истинно и второе выражение ложно.
Математические символы используются для обозначения операций и отношений, таких как равенство, неравенство, принадлежность и т.д. Например:
- Символ «=» используется для обозначения равенства двух объектов.
- Символ «≠» используется для обозначения неравенства двух объектов.
- Символ «∈» используется для обозначения принадлежности объекта к множеству.
- Символ «∧» используется для обозначения логической конъюнкции.
- Символ «∨» используется для обозначения логической дизъюнкции.
Логические и математические символы являются важным инструментом в условных обозначениях, позволяющим точно и ясно выразить отношения и операции между объектами.
Преимущества использования условных обозначений
Использование условных обозначений важно для представления объектов в различных сферах, таких как математика, программирование и логика. Они позволяют нам описывать свойства и отношения объектов на более абстрактном уровне, используя символы и знаки для задания условий и ограничений.
Преимущества использования условных обозначений включают:
- Универсальность: Условные обозначения являются универсальным средством представления объектов и связей между ними, которое можно применять в различных областях знания.
- Компактность: За счет использования символов и знаков, условные обозначения позволяют сжатое и лаконичное представление большого объема информации.
- Ясность: Условные обозначения позволяют ясно и точно описывать свойства и отношения объектов, исключая возможность различных интерпретаций или двусмысленности.
- Удобство и эффективность: Использование условных обозначений позволяет легче и быстрее описывать объекты и выполнять манипуляции с ними, особенно в случае больших данных или сложных моделей.
Улучшение понимания и восприятия информации
С помощью условных обозначений мы можем выделить ключевые аспекты объекта, добавить варианты его устройства, показать взаимосвязи и зависимости.
Улучшение понимания:
Визуализация информации через условные обозначения позволяет нам быстрее и точнее усваивать и запоминать информацию. Единичные символы и знаки, выбранные для обозначения конкретного понятия или характеристики, могут эффективно активизировать наше внимание и улучшить нашу способность к ассоциативному мышлению.
Улучшение восприятия:
Условные обозначения способны существенно упростить процесс восприятия сложной информации. Когда мы сталкиваемся с большим объемом данных или детальным описанием объекта, часто бывает сложно сразу увидеть всю картину. Однако, когда эта информация представлена с использованием условных обозначений, то мы легче выявляем главные элементы и взаимосвязи, что позволяет нам быстро ориентироваться и лучше понимать суть объекта.
В целом, использование условных обозначений позволяет нам более эффективно работать с информацией, делая ее более доступной и удобной для восприятия и понимания. Этот подход широко применяется в различных областях, включая науку, математику, информатику, дизайн, планирование и др.
Вопрос-ответ:
Что такое условные обозначения?
Условные обозначения — это символы или обозначения, которые используются для представления объектов или понятий в математике, логике, программировании и других областях. Они позволяют нам обозначать объекты и сокращать запись, что делает ее более лаконичной и понятной.
Как условные обозначения помогают представить объекты?
Условные обозначения облегчают представление объектов, поскольку они заменяют длинные и сложные описания объектов более лаконичными символами или обозначениями. Это позволяет нам более эффективно работать с объектами, а также легче выполнять математические или логические операции.
Какие области знаний используют условные обозначения?
Условные обозначения используются в различных областях знаний, включая математику, логику, физику, программирование, экономику и многие другие. В каждой из этих областей условные обозначения позволяют более компактно и точно представлять объекты и понятия, что упрощает их анализ и обработку.
Какие символы часто используются в условных обозначениях?
В условных обозначениях часто используются различные символы, такие как буквы латинского и греческого алфавитов, цифры, математические операторы и знаки препинания. Конкретные символы выбираются в зависимости от области знания и задачи, которую нужно решить с помощью условного обозначения.
Можно ли использовать свои собственные условные обозначения?
Да, можно использовать свои собственные условные обозначения. Однако, нужно быть осторожным, чтобы они были понятны для других людей, с которыми вы будете обмениваться информацией. Хорошей практикой является использование уже существующих и широко принятых условных обозначений, чтобы обеспечить единообразие и понятность вашим коммуникациям.