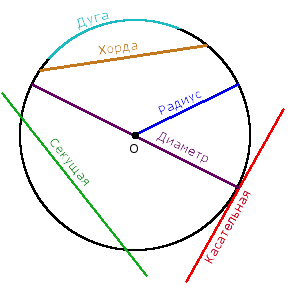
Радиус и диаметр являются основными понятиями при изучении геометрии окружностей. Радиус представляет собой отрезок, соединяющий центр окружности с любой точкой на её границе. У диаметра же есть особое значение: он равен двукратному радиусу, то есть является отрезком, проходящим через центр и состоящим из двух радиусов, противоположных друг другу.
Радиус обозначается буквой «r», а диаметр — буквой «d». Величина радиуса имеет свою собственность значение, которое отражает его длину. Величина диаметра также обладает своей длиной, которая в два раза больше радиуса. Таким образом, если радиус равен «r», то диаметр будет равен «2r». Это простая связь, позволяющая легко рассчитать диаметр окружности, зная её радиус, или наоборот.
Радиус и диаметр окружности неразрывно связаны друг с другом. Диаметр можно рассматривать как два радиуса, соединенных концами. Если описать окружность кругом, то радиус окружности будет соответствовать половине диаметра. Но важно понимать, что радиус и диаметр могут использоваться для разных целей и задач. От решаемого вопроса зависит, какую величину выбрать для своих расчетов и изображений.
Значение радиуса и диаметра окружности
Радиус окружности – это отрезок, соединяющий центр окружности и любую точку этой окружности. Обозначается символом r. Радиус окружности равен половине диаметра.
Диаметр окружности – это двукратное расстояние между точками окружности, проходящими через ее центр. Обозначается символом d. Диаметр окружности равен удвоенному радиусу.
Значение радиуса и диаметра окружности являются важными параметрами, которые используются в геометрии и других науках. Они позволяют определить геометрические свойства окружности, такие как площадь и длина окружности.
Раздел 1: Значение радиуса
Радиус обозначается буквой «r». Этот показатель показывает расстояние от центра окружности до любой точки на ее границе. Значение радиуса измеряется в тех же единицах длины, что и другие стороны фигуры.
Зная радиус окружности, можно вычислить другие характеристики, такие как диаметр, периметр и площадь. Для этого необходимо знать формулы, связывающие радиус с другими параметрами окружности. Наиболее часто используемая формула: диаметр равен удвоенному значению радиуса (D = 2r).
Таким образом, зная значение радиуса, можно определить размеры и свойства окружности без необходимости проведения сложных математических расчетов.
Подраздел 1: Определение радиуса
Значение радиуса определяется измерением длины отрезка, соединяющего центр окружности с любой ее точкой. Радиус измеряется в единицах длины, например, в метрах или сантиметрах, в зависимости от системы измерения.
Радиус окружности является важным параметром при решении геометрических задач. Он используется для вычисления площади и длины окружности, а также для определения других свойств и характеристик окружности.
| Символ | Описание |
|---|---|
| r | радиус окружности |
Подраздел 2: Измерение радиуса
Одним из наиболее распространенных инструментов для измерения радиуса является циркуль. Циркуль представляет собой инструмент с двумя ногами, одна из которых фиксирована, а другая может перемещаться вдоль окружности. Путем установки ножек циркуля на противоположные концы окружности и измерения расстояния между ними можно получить значение радиуса.
Для более точных измерений радиуса могут использоваться специализированные инструменты, такие как микрометр или штангенциркуль. Эти инструменты позволяют измерить радиус с более высокой точностью и могут использоваться в производственных и научных целях.
Измерение радиуса является важным шагом при работе с окружностями, поскольку радиус определяет множество свойств окружности, таких как ее длина (длина окружности равна удвоенному произведению радиуса на число π), площадь (площадь окружности равна произведению радиуса на себя и число π) и центр окружности.
Измерение радиуса является фундаментальным понятием в геометрии и нашло широкое применение в математике, физике, инженерии и многих других научных и прикладных областях. Правильное измерение радиуса позволяет точно определить размеры и характеристики окружности и использовать эту информацию в различных практических задачах.
Раздел 2: Значение диаметра
Для расчета диаметра достаточно знать значение радиуса. Диаметр равен удвоенному значению радиуса. Таким образом, если радиус окружности равен 5 см, то ее диаметр будет равен 10 см.
Величина диаметра имеет важное значение при решении геометрических задач. Она определяет такие характеристики окружности, как ее длина, площадь, а также периметр окружности.
Более того, диаметр является основой для определения других характеристик окружности, например, радиуса или дуги. Известно, что диаметр равен сумме двух радиусов, а также в два раза превышает длину дуги, соответствующей половине окружности.
Таким образом, для полного анализа и понимания свойств окружности необходимо учитывать значение и взаимосвязь с радиусом и другими характеристиками. Диаметр имеет большое значение в геометрии и применяется в различных сферах науки и техники.
Подраздел 1: Определение диаметра
Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Диаметр является наибольшим отрезком в окружности и делит ее на две равные части.
Диаметр можно определить с помощью радиуса окружности, поскольку радиус и диаметр связаны формулой: диаметр = 2 * радиус.
Выбирая две точки на окружности и измеряя расстояние между ними, мы сможем определить диаметр окружности. Определение диаметра важно для многих математических расчетов и построений, связанных с окружностями.
Подраздел 2: Измерение диаметра
Для измерения диаметра при помощи линейки необходимо разместить ее параллельно окружности и замерить расстояние между двумя противоположными точками. Однако такой способ измерения может быть неточным из-за возможной погрешности приложения линейки.
Более точный способ измерения диаметра осуществляется с помощью штангенциркуля или микрометра. Для этого необходимо приложить измерительный инструмент к окружности так, чтобы одна его пластина касалась одной стороны окружности, а другая – противоположной. Затем, перемещая инструмент по окружности, нужно зафиксировать на шкале или экране измерительного прибора значение диаметра окружности.
Измерение диаметра окружности позволяет вычислить значение других геометрических свойств, таких как радиус, площадь или длина окружности. Диаметр также является важной характеристикой при решении различных задач в физике, механике, астрономии и других областях науки.
Раздел 3: Взаимосвязь радиуса и диаметра
Между радиусом и диаметром существует определенная взаимосвязь. Диаметр можно выразить через радиус по формуле:
Д = 2R
где Д — диаметр, R — радиус.
То есть, чтобы найти диаметр окружности, нужно умножить ее радиус на 2. Это связано с тем, что диаметр — это двойная длина радиуса.
С другой стороны, радиус можно найти, разделив диаметр на 2:
R = Д / 2
Таким образом, радиус можно найти, зная диаметр окружности, путем деления этой величины на 2.
Важно отметить, что диаметр и радиус являются величинами, измеряемыми в одной и той же единице длины, например, в сантиметрах или метрах. Зная лишь одну из этих характеристик, можно вычислить другую. Их взаимосвязь позволяет удобно работать с окружностями и проводить различные геометрические расчеты.
Подраздел 1: Формула взаимосвязи
Диаметр (D) равен удвоенному значению радиуса (R):
D = 2R
Это означает, что диаметр окружности всегда равен удвоенному значению радиуса.
Учитывая это соотношение, можно легко выразить радиус через диаметр:
R = D/2
Таким образом, радиус окружности равен половине ее диаметра. Эта формула позволяет удобно переходить от одного параметра к другому.
Вопрос-ответ:
Что такое радиус окружности и как он определяется?
Радиус окружности — это отрезок, соединяющий центр окружности с любой точкой на ней. Радиус определяется как половина диаметра окружности.
Какое значение имеет радиус окружности?
Радиус окружности имеет значение для определения ее размера, формы и свойств. Он используется, например, для вычисления площади и длины окружности.
Как радиус влияет на окружность?
Радиус окружности определяет ее размер. Чем больше радиус, тем больше окружность, и наоборот. Радиус также влияет на площадь и длину окружности.
Какова взаимосвязь между радиусом и диаметром окружности?
Диаметр окружности равен удвоенному радиусу. То есть, если радиус равен R, то диаметр равен 2R. Это означает, что радиус и диаметр связаны простым соотношением — диаметр равен двум радиусам.
Для чего нужно знать радиус и диаметр окружности?
Знание радиуса и диаметра окружности позволяет решать различные задачи в геометрии, а также применять их в практических ситуациях. Например, они могут быть использованы для вычисления площади круга, нахождения длины окружности, построения графиков и т.д.
Чем отличается радиус окружности от диаметра?
Радиус окружности — это отрезок, соединяющий центр окружности с любой точкой на ее окружности. Диаметр окружности — это отрезок, соединяющий две противоположные точки на ее окружности и проходящий через ее центр.
Зачем нужны радиус и диаметр окружности?
Радиус и диаметр окружности имеют важное значение в геометрии и в решении различных задач. Они используются для вычисления площади и длины окружности, а также для определения свойств и характеристик фигур, которые связаны с окружностью.