Система счисления – один из ключевых элементов математики, который позволяет представить числа с помощью определенных символов и правил. Она является основой для работы с числами и выполняет важную роль в различных научных дисциплинах, включая физику, информатику и экономику.
Знаки числа – это важная часть системы счисления, которая указывает на положительность или отрицательность числа. Когда мы говорим о положительных числах, знак перед числом обычно не указывается. Но когда речь идет об отрицательных числах, перед числом ставится минус (-) в качестве знака. Наличие знаков числа позволяет нам легко определить их значения и проводить различные операции с числами.
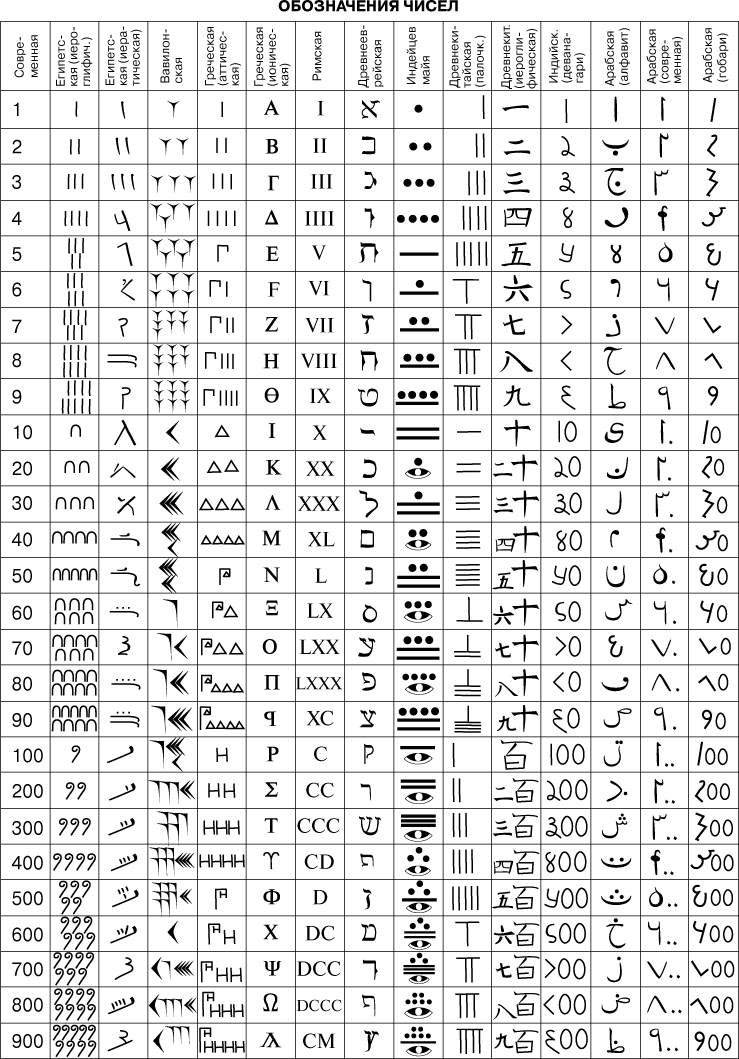
Алфавит цифр – это определенный набор символов, которые используются для представления чисел в системе счисления. В наиболее распространенной системе счисления – десятичной – алфавит цифр состоит из десяти символов: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Каждая цифра имеет свое значение в зависимости от ее положения в числе. Например, в числе 123 цифра 1 означает 100, цифра 2 означает 20, а цифра 3 означает 3.
Понимание системы счисления, знаков числа и алфавита цифр является важной предпосылкой для понимания основ математики и работы с числами. Эти концепции не только помогают нам считать, но и дают нам возможность представлять и анализировать различные величины и явления с помощью числовых данных.
Система счисления: знаки, числа и алфавит цифр
Значение числа в системе счисления определяется не только цифрами, но и их порядком следования. В зависимости от системы счисления, каждая цифра имеет свое значение. Например, в десятичной системе счисления, мы используем цифры от 0 до 9, где каждая цифра имеет значение, соответствующее ее позиции в числе.
Одна из важных составляющих системы счисления — знак числа. Знак числа указывает, положительное оно или отрицательное. В математике принято считать, что положительные числа не имеют знакового символа, а отрицательные числа обозначаются знаком минус («-«).
Алфавит цифр — это набор символов, которыми можно представить числа в системе счисления. Например, в десятичной системе счисления мы используем десять символов от 0 до 9. В других системах счисления могут использоваться другие символы, например, в двоичной системе счисления мы используем только две цифры — 0 и 1.
Использование системы счисления позволяет нам работать с числами разных величин и значений. Она находит широкое применение в различных областях, включая математику, физику, компьютерные науки и технологии.
Знаки в системе счисления
В системе счисления каждое число обозначается определенным набором символов. В зависимости от используемой системы счисления, эти символы могут иметь различные значения и допускать определенные ограничения.
Одним из важных компонентов системы счисления является знак числа. Знак числа показывает, является ли число положительным, отрицательным или нулем. В большинстве систем счисления используется знак «+» для обозначения положительных чисел и знак «-» для обозначения отрицательных чисел. Ноль, как правило, не имеет специального знака и считается нейтральным.
Знак числа имеет большое значение при выполнении различных операций, таких как сложение, вычитание, умножение и деление. Знак числа также определяет область применения числа в различных математических и физических контекстах.
Помимо знака числа, система счисления также имеет алфавит цифр. Алфавит цифр представляет собой набор символов, которые используются для обозначения различных значений в числе. Наиболее распространенным алфавитом цифр является десятичный алфавит, который состоит из цифр от 0 до 9. Однако существуют и другие системы счисления, которые используют разные алфавиты цифр, например двоичный алфавит (0 и 1), восьмеричный алфавит (0-7) и шестнадцатеричный алфавит (0-9, A-F).
Знаки числа и алфавит цифр являются основными компонентами системы счисления и позволяют нам представлять различные значения в удобной и компактной форме. Наличие знаков и разнообразие алфавитов цифр делает системы счисления мощным инструментом, который применяется в различных областях науки, техники и повседневной жизни.
Значение и применение знаков
Знаки числа используются для обозначения направления или ориентации величины. Зачастую они вносят ясность и позволяют нам легче интерпретировать информацию. Например, в физике минусовой знак часто указывает на противоположное направление движения, отрицательное значение температуры или энергии.
В программировании отрицательные знаки широко используются для кодирования отрицательных чисел и логических состояний. Бит знака может указывать на положение числа относительно нуля (отрицательное или положительное) или выполнять функцию флага, сигнализирующего о выполнении определенного условия.
Знаки чисел также имеют практическое применение в повседневной жизни. Например, в бухгалтерии они помогают различать положительные и отрицательные значения денежных сумм или балансов на счетах. В логистике они указывают на приход или убыль товаров на складе. В календарях отрицательные значения могут указывать на отсутствие событий или недоступные времярабочие дни.
Таким образом, знаки числа являются важным и неотъемлемым элементом системы счисления. Они помогают нам понимать и интерпретировать числовые значения, а также находят широкое применение в различных областях науки, техники и повседневной жизни.
Роли знаков в математике
Знаки играют важную роль в математике и помогают нам представлять и описывать различные концепции и операции. Они позволяют нам выражать положительные и отрицательные значения, указывать на операции сложения, вычитания, умножения и деления, а также определять и отделять различные компоненты в уравнениях и выражениях.
Знак «+» используется для обозначения сложения и положительных значений. Он позволяет нам объединять числа и признаки, указывая на то, что значения складываются вместе.
Знак «-» используется для обозначения вычитания, отрицательных значений и разности между двумя числами. Он указывает на противоположность или отсутствие величины.
Знак «*» используется для обозначения умножения и показывает, что значения умножаются друг на друга или повторяются.
Знак «/» используется для обозначения деления и показывает, что одно значение разделено на другое.
Знаки «(«, «)» и «[» «]» используются для группировки и отделения различных компонентов в уравнениях и выражениях. Они помогают нам понять порядок выполнения операций и структуру математических выражений.
Знаки «>», «<", ">=», «<=" используются для сравнения двух значений. Они позволяют нам определить, какое значение больше или меньше, а также указывают на отношение между двумя числами.
Знаки «=» и «≠» используются для сравнения равенства и неравенства двух значений. Они позволяют нам утверждать или опровергать равенство между двуми числами или выражениями.
Знаки «±» и «∓» используются для указания на возможные значения с разными знаками. Они позволяют нам указывать на то, что числа могут быть как положительными, так и отрицательными.
В математике знаки играют важную роль в создании и понимании математических выражений, уравнений и неравенств. Они позволяют нам точно и ясно выражать и описывать различные математические концепции и операции, что является основой для решения задач и исследований в этой науке.
Примеры знаков в различных системах счисления
Представление знака числа может отличаться в различных системах счисления. Например, в десятичной системе счисления знак числа может быть положительным (+) или отрицательным (-). В двоичной системе счисления знак числа также может быть положительным или отрицательным, но здесь он обычно представляется дополнительным кодом.
Примеры знаков числа в различных системах счисления:
- Десятичная система счисления: позитивное число +3, отрицательное число -7
- Двоичная система счисления: позитивное число 0101, отрицательное число 1010 (в дополнительном коде)
- Восьмеричная система счисления: позитивное число 0123, отрицательное число -0765
- Шестнадцатеричная система счисления: позитивное число 0xAB, отрицательное число -0xCD (в дополнительном коде)
Знак числа играет важную роль в математических операциях и позволяет определить значение числа в контексте данной системы счисления.
Числа в системе счисления
Наиболее распространенной системой счисления является десятичная система, в которой используются цифры от 0 до 9. В десятичной системе каждая позиция числа имеет вес, который определяется мощностью десяти. Например, число 256 можно разложить на сумму произведений цифр на соответствующие веса: 2 × 10² + 5 × 10¹ + 6 × 10⁰.
Однако, существуют и другие системы счисления, такие как двоичная, восьмеричная и шестнадцатеричная. В двоичной системе счисления используются только две цифры: 0 и 1. В восьмеричной системе счисления используются цифры от 0 до 7. В шестнадцатеричной системе счисления используются цифры от 0 до 9 и буквы от A до F, которые обозначают числа от 10 до 15.
Перевод чисел из одной системы счисления в другую осуществляется путем разложения числа по разрядам и умножения цифр на соответствующие веса. Кроме того, существует возможность использования отрицательных чисел, для которых используются знаки числа: «+» и «−». Знак числа указывает на его положительное или отрицательное значение.
Использование различных систем счисления имеет свои особенности и применения в разных областях. Например, двоичная система счисления широко применяется в компьютерной технике для представления и обработки информации, так как компьютеры основаны на электронных элементах, которые имеют два стабильных состояния – включено и выключено.
Важно понимать, что системы счисления – это лишь способ представления чисел, и каждая из них имеет свои преимущества и особенности. Познакомиться с принципами работы различных систем счисления поможет лучшему пониманию базовых математических концепций и их применения в реальных ситуациях.
Отличия чисел в разных системах счисления
Системы счисления позволяют представлять числа в различных форматах в зависимости от основания системы. Основания систем могут быть разными, обычно используются десятичная, двоичная, восьмеричная и шестнадцатеричная.
Одно из основных отличий между разными системами счисления — количество доступных цифр или символов. В десятичной системе используются десять цифр от 0 до 9, в двоичной — две цифры 0 и 1, в восьмеричной — восемь цифр от 0 до 7, а в шестнадцатеричной — шестнадцать символов от 0 до 9 и от A до F.
Другое отличие заключается в значении каждой цифры в числе. В десятичной системе значение цифры зависит от ее позиции в числе. Например, цифра 5 в числе 546 имеет значение 500, цифра 4 — 40 и цифра 6 — 6. В двоичной системе каждая цифра также имеет вес в зависимости от ее позиции, но в двоичной системе весы цифр являются степенями числа 2.
Еще одно отличие состоит в способе записи чисел. В десятичной системе числа записываются слева направо, начиная с наибольшей значащей цифры. В двоичной системе числа также записываются слева направо, но используется только 0 и 1. В восьмеричной и шестнадцатеричной системах цифры также записываются слева направо, но в отличие от двоичной системы используются больше цифр или символов для представления чисел.
Важно также отметить, что числа в разных системах счисления могут иметь разное представление и длину. Например, число 10 в двоичной системе представляется как 1010, а в восьмеричной системе — как 12. Также некоторые числа могут иметь бесконечное количество знаков после запятой в десятичной системе, но представляться конечным количеством знаков в двоичной или других системах.
Таким образом, отличия чисел в разных системах счисления заключаются в количестве и значении цифр, способе записи и длине представления чисел.
Примеры чисел в различных системах счисления
Вот несколько примеров чисел в различных системах счисления:
| Система счисления | Пример числа | Значение |
|---|---|---|
| Десятичная | 42 | Сорок два |
| Двоичная | 1010 | Десять |
| Шестнадцатеричная | FF | Двести пятьдесят пять |
Как видно из примеров, числа в разных системах счисления могут иметь различные значения, даже при одинаковой записи. Поэтому важно учитывать систему счисления при работе с числами, особенно при переводе значений из одной системы в другую.
Как переводить числа из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую может быть достаточно сложным процессом, но с некоторыми основными правилами и шагами его можно освоить.
Вот простая инструкция по переводу чисел из одной системы счисления в другую:
- Определите значение исходного числа в десятичной системе счисления. Для этого умножьте каждую цифру числа на степень основания системы счисления и сложите полученные значения.
- Определите основание новой системы счисления, в которую вы хотите перевести число.
- Разделите полученное в первом шаге значение на основание новой системы счисления. Запишите остаток от деления, это будет крайняя правая цифра нового числа.
- Поделите полученное в предыдущем шаге значение на основание новой системы счисления и опять запишите остаток от деления.
- Продолжайте делить полученное значение до тех пор, пока оно не станет равным нулю. Все полученные остатки записывайте слева направо. Это будет новое число в новой системе счисления.
Пример:
Давайте переведем число 101 из двоичной системы в десятичную. Следуя инструкции:
- Умножаем каждую цифру числа на степень основания (2) и складываем полученные значения: 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 5
- Определяем основание новой системы счисления, в данном случае это 10 (десятичная система).
- Делим полученное значение (5) на основание новой системы и получаем остаток: 5 % 10 = 5. Первая цифра нового числа будет 5.
После этого продолжаем делить 5 на 10 и получаем остаток 5. Поскольку остаток равен исходному числу, процесс завершается и новое число в десятичной системе счисления будет таким же: 101.
Таким образом, следуя инструкции, вы сможете переводить числа из одной системы счисления в другую без особых сложностей.
Вопрос-ответ:
Что такое система счисления?
Система счисления — это способ представления чисел с помощью цифр. Она определяет правила записи чисел и операций над ними. Наиболее распространенные системы счисления — десятичная (основание 10) и двоичная (основание 2).
Что такое знаки числа в системе счисления?
Знак числа в системе счисления указывает на его положительность или отрицательность. В десятичной системе счисления знак числа обычно записывается перед числом как символ «+» для положительных чисел и «-» для отрицательных чисел.
Что такое алфавит цифр в системе счисления?
Алфавит цифр в системе счисления — это набор символов (цифр), которые используются для записи чисел. В десятичной системе счисления алфавит цифр состоит из десяти символов от 0 до 9, а в двоичной системе счисления алфавит цифр состоит из двух символов — 0 и 1.
Какие еще системы счисления существуют?
Помимо десятичной и двоичной, существуют и другие системы счисления. Например, в восьмеричной системе счисления основание равно 8, а алфавит цифр состоит из восьми символов от 0 до 7. В шестнадцатеричной системе счисления основание равно 16, а алфавит цифр состоит из шестнадцати символов от 0 до 9 и от A до F.